给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表words,返回所有二维网格上的单词 。
单词必须按照字母顺序,通过 相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例 1:
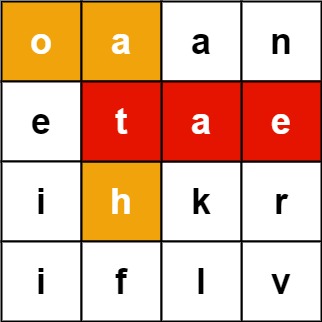
输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出:["eat","oath"]
示例 2:
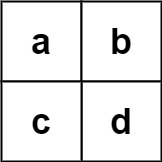
输入:board = [["a","b"],["c","d"]], words = ["abcb"]
输出:[]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]是一个小写英文字母- \(1 <= words.length <= 3 * 10^4\)
1 <= words[i].length <= 10words[i]由小写英文字母组成words中的所有字符串互不相同
题解
方法一:回溯 + 字典树
思路和算法
根据题意,我们需要逐个遍历二维网格中的每一个单元格;然后搜索从该单元格出发的所有路径,找到其中对应 \(\textit{words}\) 中的单词的路径。因为这是一个回溯的过程,所以我们有如下算法:
遍历二维网格中的所有单元格。
深度优先搜索所有从当前正在遍历的单元格出发的、由相邻且不重复的单元格组成的路径。因为题目要求同一个单元格内的字母在一个单词中不能被重复使用;所以我们在深度优先搜索的过程中,每经过一个单元格,都将该单元格的字母临时修改为特殊字符(例如
#),以避免再次经过该单元格。如果当前路径是 \(\textit{words}\) 中的单词,则将其添加到结果集中。如果当前路径是 \(words\) 中任意一个单词的前缀,则继续搜索;反之,如果当前路径不是 \(words\) 中任意一个单词的前缀,则剪枝。我们可以将 \(\textit{words}\) 中的所有字符串先添加到前缀树中,而后用 \(O(|S|)\) 的时间复杂度查询当前路径是否为 \(\textit{words}\) 中任意一个单词的前缀。
在具体实现中,我们需要注意如下情况:
因为同一个单词可能在多个不同的路径中出现,所以我们需要使用哈希集合对结果集去重。
在回溯的过程中,我们不需要每一步都判断完整的当前路径是否是 \(words\) 中任意一个单词的前缀;而是可以记录下路径中每个单元格所对应的前缀树结点,每次只需要判断新增单元格的字母是否是上一个单元格对应前缀树结点的子结点即可。
代码
class Solution {
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
Set<String> ans = new HashSet<String>();
for (int i = 0; i < board.length; ++i) {
for (int j = 0; j < board[0].length; ++j) {
dfs(board, trie, i, j, ans);
}
}
return new ArrayList<String>(ans);
}
public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
if (!now.children.containsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
now = now.children.get(ch);
if (!"".equals(now.word)) {
ans.add(now.word);
}
board[i1][j1] = '#';
for (int[] dir : dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
dfs(board, now, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
}
class Trie {
String word;
Map<Character, Trie> children;
boolean isWord;
public Trie() {
this.word = "";
this.children = new HashMap<Character, Trie>();
}
public void insert(String word) {
Trie cur = this;
for (int i = 0; i < word.length(); ++i) {
char c = word.charAt(i);
if (!cur.children.containsKey(c)) {
cur.children.put(c, new Trie());
}
cur = cur.children.get(c);
}
cur.word = word;
}
}
复杂度分析
时间复杂度:\(O(m \times n \times 3^{l-1})\),其中 \(m\) 是二维网格的高度,\(n\) 是二维网格的宽度,\(l\) 是最长单词的长度。我们需要遍历 \(m \times n\) 个单元格,每个单元格最多需要遍历 \(4 \times 3^{l-1}\) 条路径。
空间复杂度:\(O(k \times l)\),其中 \(k\) 是 \(\textit{words}\) 的长度,\(l\) 是最长单词的长度。最坏情况下,我们需要 \(O(k \times l)\) 用于存储前缀树。
方法二:删除被匹配的单词
思路和算法
考虑以下情况。假设给定一个所有单元格都是 a 的二维字符网格和单词列表 ["a", "aa", "aaa", "aaaa"] 。当我们使用方法一来找出所有同时在二维网格和单词列表中出现的单词时,我们需要遍历每一个单元格的所有路径,会找到大量重复的单词。
为了缓解这种情况,我们可以将匹配到的单词从前缀树中移除,来避免重复寻找相同的单词。因为这种方法可以保证每个单词只能被匹配一次;所以我们也不需要再对结果集去重了。
代码
class Solution {
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
Set<String> ans = new HashSet<String>();
for (int i = 0; i < board.length; ++i) {
for (int j = 0; j < board[0].length; ++j) {
dfs(board, trie, i, j, ans);
}
}
return new ArrayList<String>(ans);
}
public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
if (!now.children.containsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
Trie nxt = now.children.get(ch);
if (!"".equals(nxt.word)) {
ans.add(nxt.word);
nxt.word = "";
}
if (!nxt.children.isEmpty()) {
board[i1][j1] = '#';
for (int[] dir : dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
dfs(board, nxt, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
if (nxt.children.isEmpty()) {
now.children.remove(ch);
}
}
}
class Trie {
String word;
Map<Character, Trie> children;
boolean isWord;
public Trie() {
this.word = "";
this.children = new HashMap<Character, Trie>();
}
public void insert(String word) {
Trie cur = this;
for (int i = 0; i < word.length(); ++i) {
char c = word.charAt(i);
if (!cur.children.containsKey(c)) {
cur.children.put(c, new Trie());
}
cur = cur.children.get(c);
}
cur.word = word;
}
}
复杂度分析
时间复杂度:\(O(m \times n \times 3^{l-1})\),其中 \(m\) 是二维网格的高度,\(n\) 是二维网格的宽度,\(l\) 是最长单词的长度。我们仍需要遍历 \(m \times n\) 个单元格,每个单元格在最坏情况下仍需要遍历 \(4 \times 3^{l-1}\) 条路径。
空间复杂度:\(O(k \times l)\),其中 \(k\) 是 \(\textit{words}\) 的长度,\(l\) 是最长单词的长度。最坏情况下,我们需要 \(O(k \times l)\) 用于存储前缀树。