LeetCode 560. Subarray Sum Equals K - Harp Seal Pup Nursery and Caring Center

Given an array of integers nums and an integer k, return the total number of subarrays whose sum equals to k.

A subarray is a contiguous non-empty sequence of elements within an array.

Example 1:

Input: nums = [1,1,1], k = 2
Output: 2

Example 2:

Input: nums = [1,2,3], k = 3
Output: 2

Constraints:

$1 \le nums.length \le 2 \times 10^4$
$-1000 \le nums[i] \le 1000$
$-10^7 \le k \le 10^7$

题解

方法一：枚举

思路和算法

考虑以 $i$ 结尾和为 $k$ 的连续子数组个数，我们需要统计符合条件的下标 $j$ 的个数，其中 $0\leq j\leq i$ 且 $[j..i]$ 这个子数组的和恰好为 $k$ 。

我们可以枚举 $[0..i]$ 里所有的下标 $j$ 来判断是否符合条件，可能有读者会认为假定我们确定了子数组的开头和结尾，还需要 $O(n)$ 的时间复杂度遍历子数组来求和，那样复杂度就将达到 $O(n^3)$ 从而无法通过所有测试用例。但是如果我们知道 $[j,i]$ 子数组的和，就能 $O(1)$ 推出 $[j-1,i]$ 的和，因此这部分的遍历求和是不需要的，我们在枚举下标 $j$ 的时候已经能 $O(1)$ 求出 $[j,i]$ 的子数组之和。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.size(); ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
};

复杂度分析

时间复杂度：$O(n^2)$，其中 $n$ 为数组的长度。枚举子数组开头和结尾需要 $O(n^2)$ 的时间，其中求和需要 $O(1)$ 的时间复杂度，因此总时间复杂度为 $O(n^2)$。
空间复杂度：$O(1)$。只需要常数空间存放若干变量。

方法二：前缀和 + 哈希表优化

思路和算法

我们可以基于方法一利用数据结构进行进一步的优化，我们知道方法一的瓶颈在于对每个 $i$，我们需要枚举所有的 $j$ 来判断是否符合条件，这一步是否可以优化呢？答案是可以的。

我们定义 $\textit{pre}[i]$ 为 $[0..i]$ 里所有数的和，则 $\textit{pre}[i]$ 可以由 $\textit{pre}[i-1]$ 递推而来，即：

$$\textit{pre}[i]=\textit{pre}[i-1]+\textit{nums}[i]$$

那么「$[j..i]$ 这个子数组和为 $k$ 」这个条件我们可以转化为

$$\textit{pre}[i]-\textit{pre}[j-1]==k$$

简单移项可得符合条件的下标 $j$ 需要满足

$$\textit{pre}[j-1] == \textit{pre}[i] - k$$

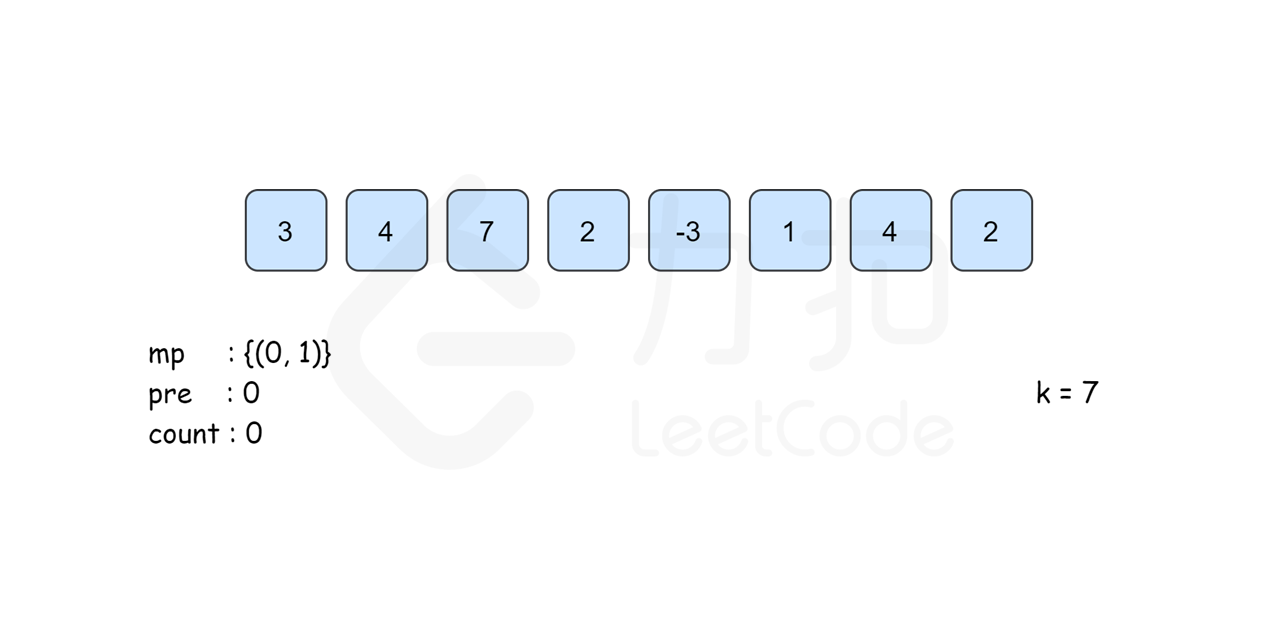
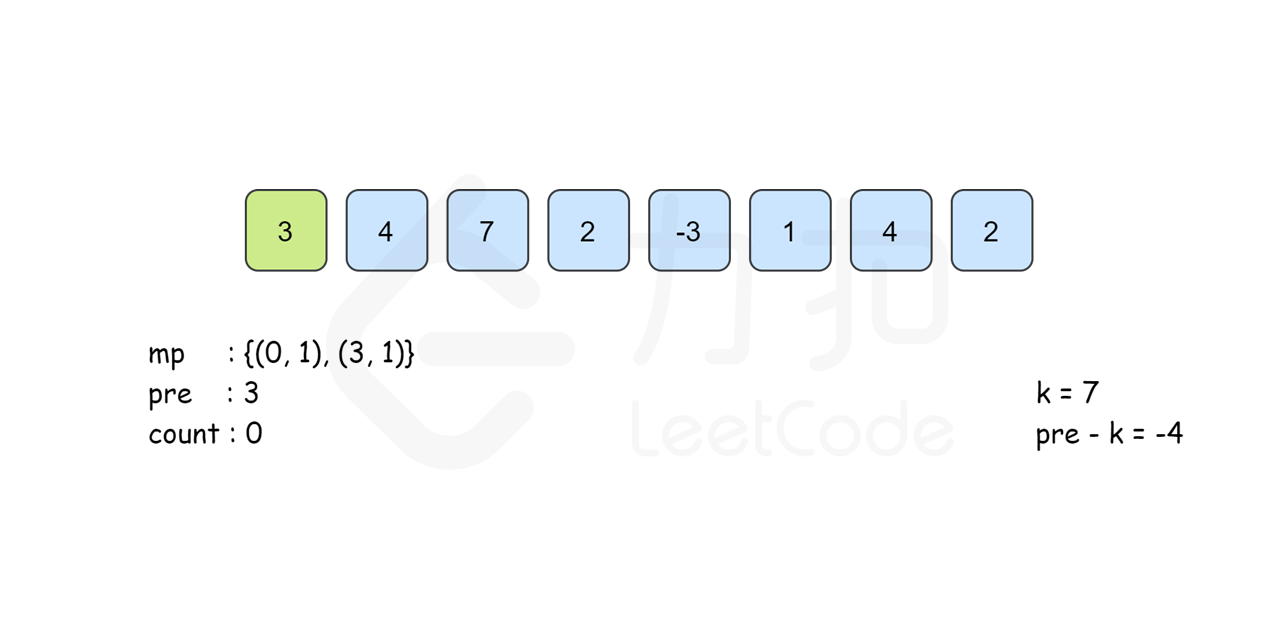
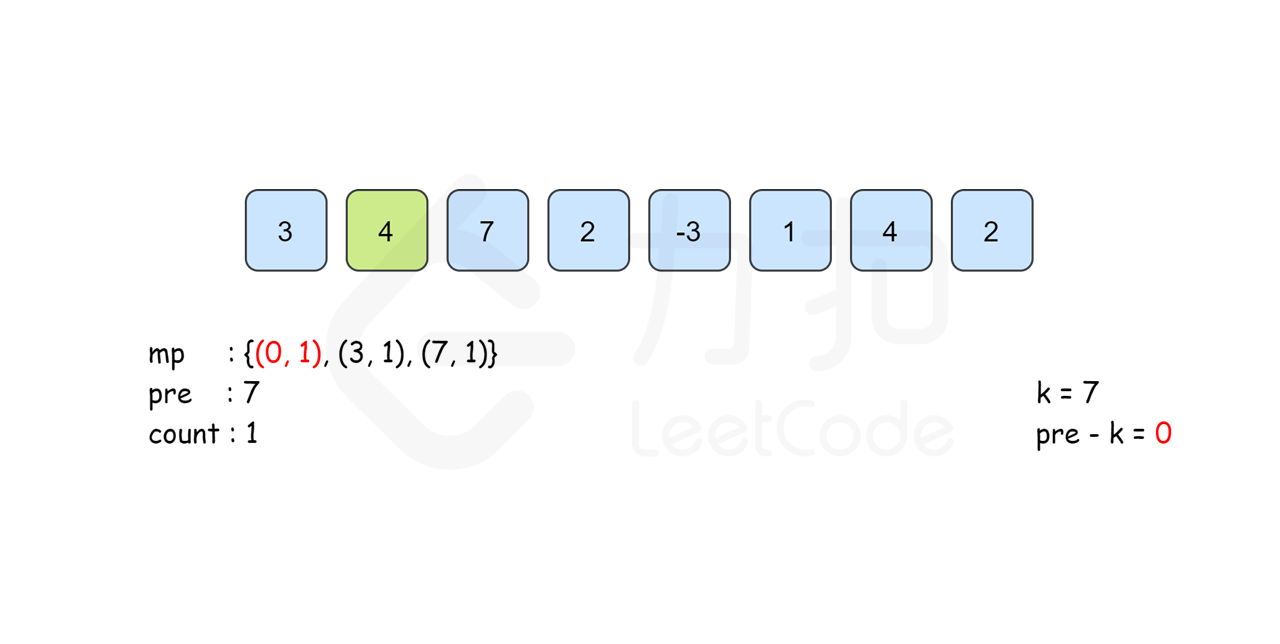
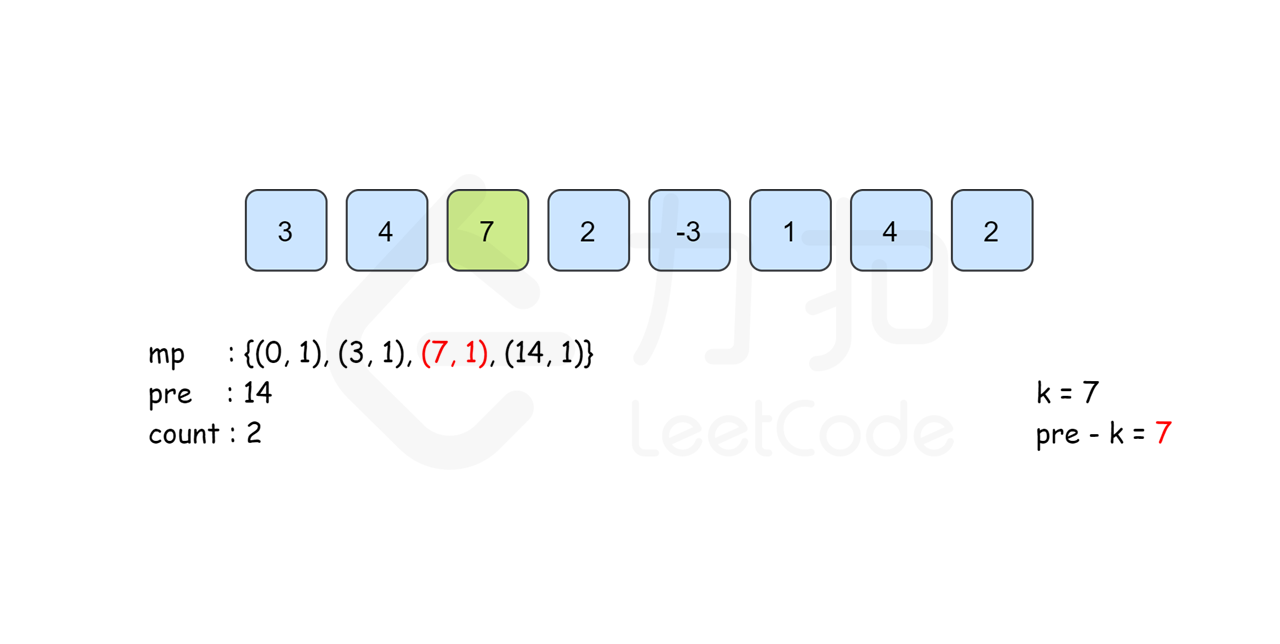
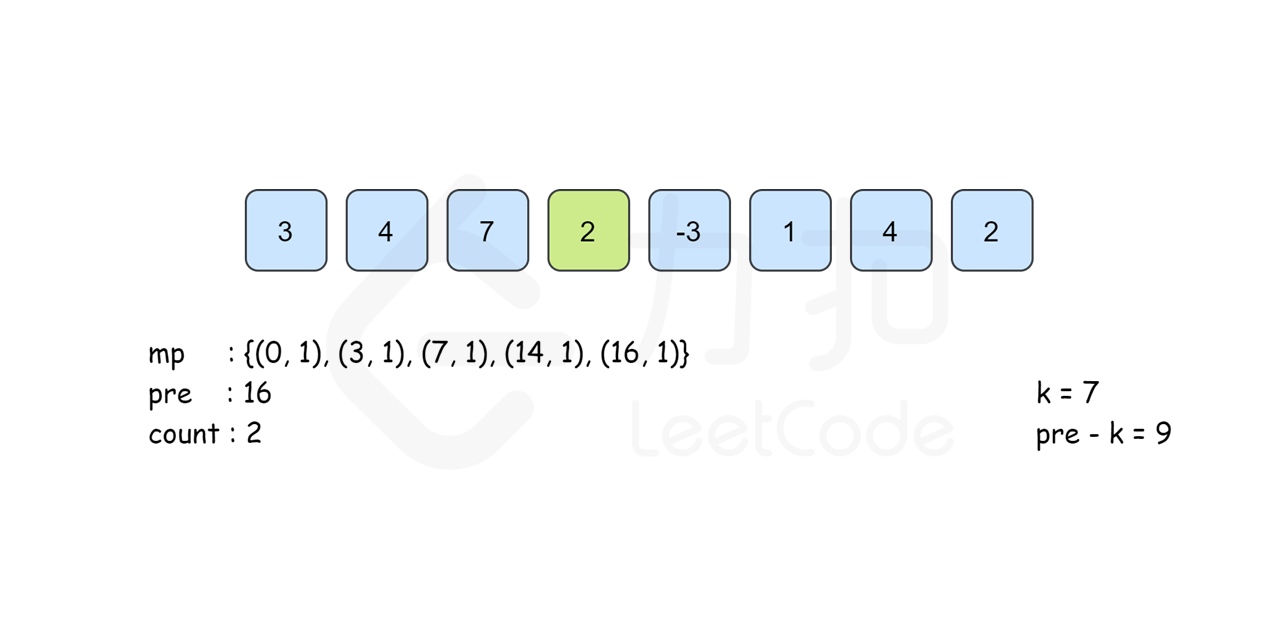
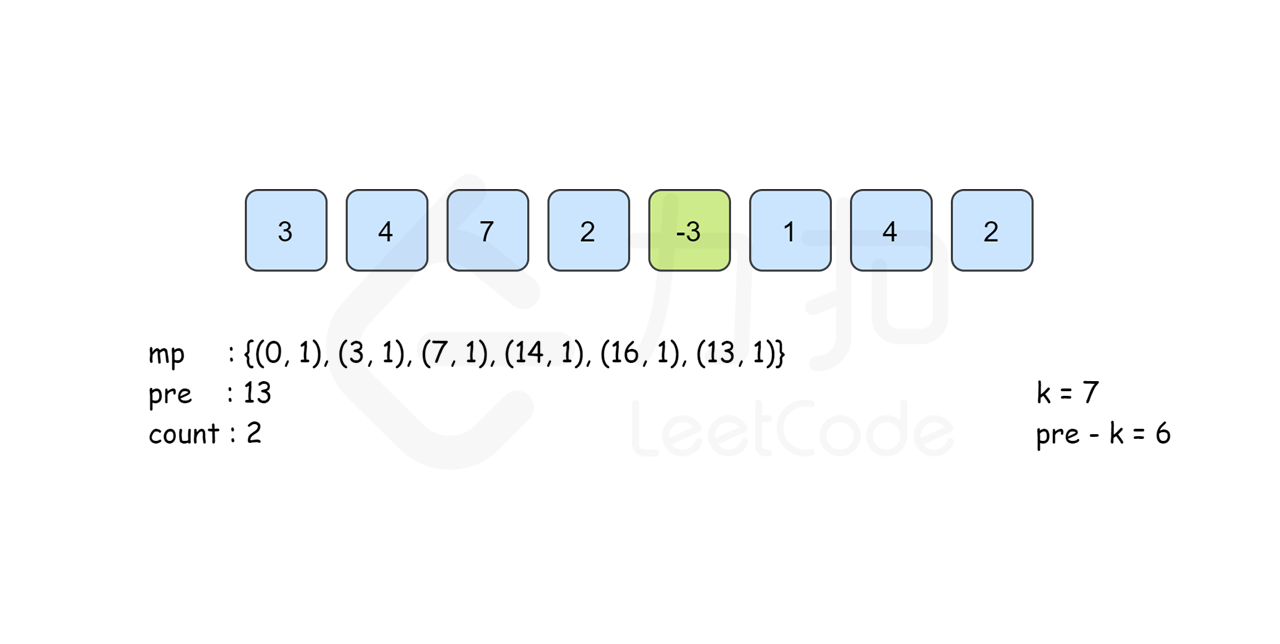
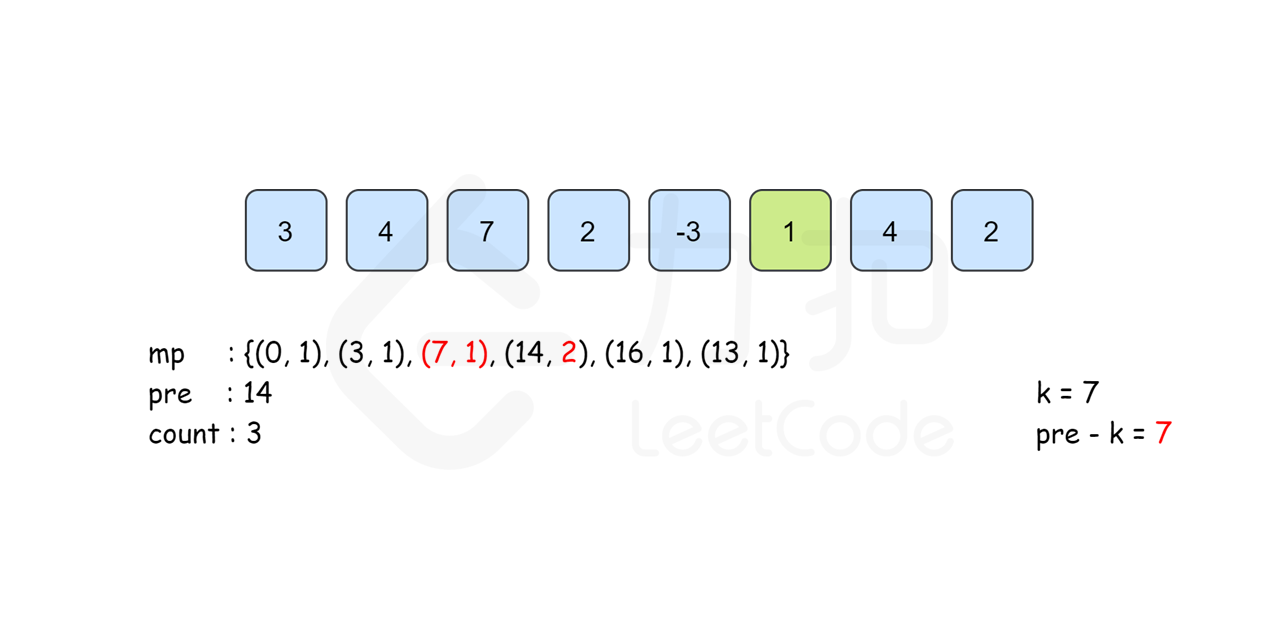
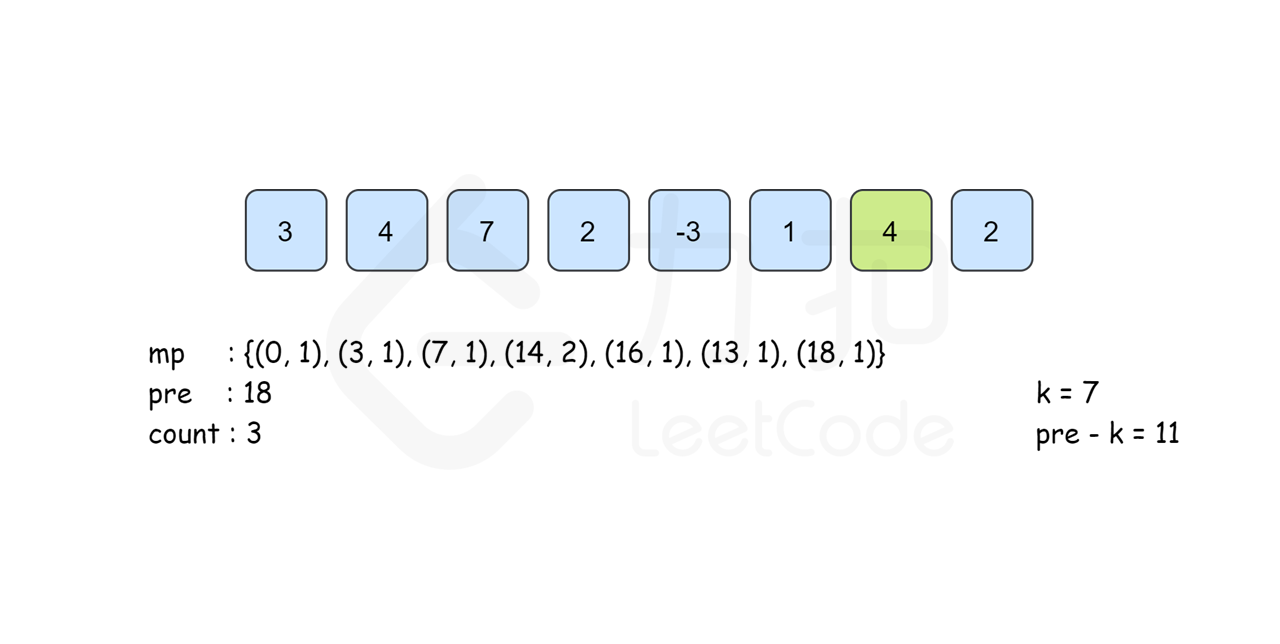
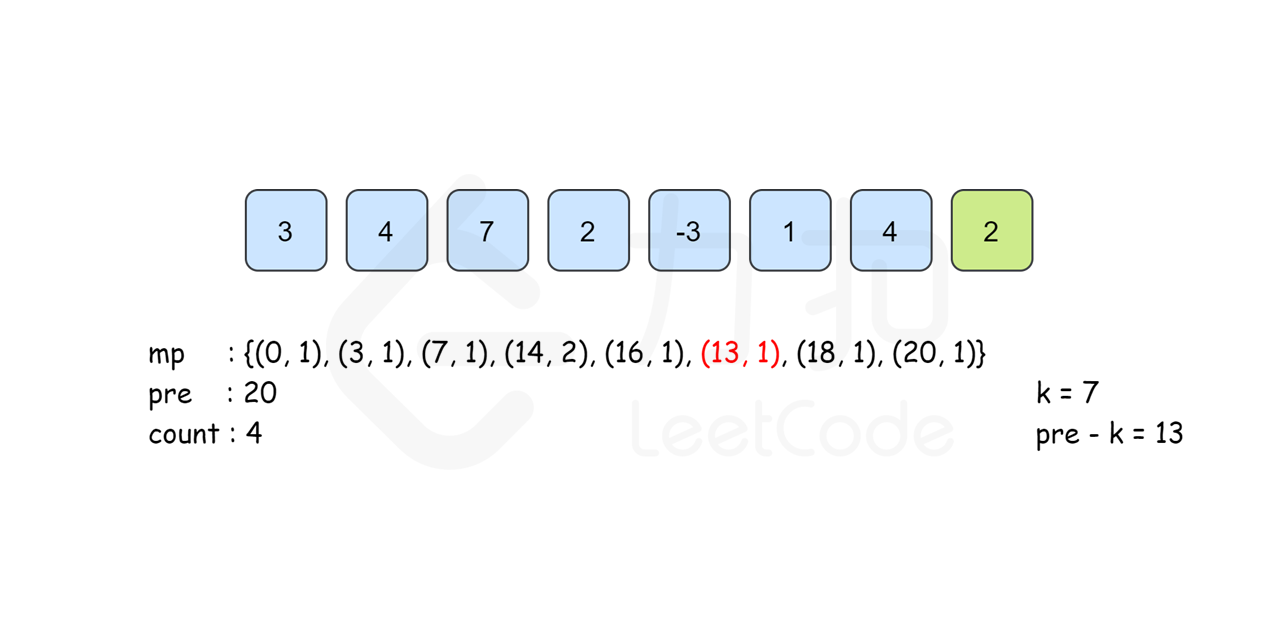
所以我们考虑以 $i$ 结尾的和为 $k$ 的连续子数组个数时只要统计有多少个前缀和为 $\textit{pre}[i]-k$ 的 $\textit{pre}[j]$ 即可。我们建立哈希表 $\textit{mp}$，以和为键，出现次数为对应的值，记录 $\textit{pre}[i]$ 出现的次数，从左往右边更新 $\textit{mp}$ 边计算答案，那么以 $i$ 结尾的答案 $\textit{mp}[\textit{pre}[i]-k]$ 即可在 $O(1)$ 时间内得到。最后的答案即为所有下标结尾的和为 $k$ 的子数组个数之和。

需要注意的是，从左往右边更新边计算的时候已经保证了$\textit{mp}[\textit{pre}[i]-k]$ 里记录的 $\textit{pre}[j]$ 的下标范围是 $0\leq j\leq i$ 。同时，由于$\textit{pre}[i]$ 的计算只与前一项的答案有关，因此我们可以不用建立 $\textit{pre}$ 数组，直接用 $\textit{pre}$ 变量来记录 $pre[i-1]$ 的答案即可。

fig1

fig2

fig3

fig4

fig5

fig6

fig7

fig8

fig9

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        mp[0] = 1;
        int count = 0, pre = 0;
        for (auto& x:nums) {
            pre += x;
            if (mp.find(pre - k) != mp.end()) {
                count += mp[pre - k];
            }
            mp[pre]++;
        }
        return count;
    }
};

复杂度分析

时间复杂度：$O(n)$，其中 $n$ 为数组的长度。我们遍历数组的时间复杂度为 $O(n)$，中间利用哈希表查询删除的复杂度均为 $O(1)$，因此总时间复杂度为 $O(n)$。
空间复杂度：$O(n)$，其中 $n$ 为数组的长度。哈希表在最坏情况下可能有 $n$ 个不同的键值，因此需要 $O(n)$ 的空间复杂度

azarasi / LeetCode 560. Subarray Sum Equals K

题解

方法一：枚举

方法二：前缀和 + 哈希表优化