LeetCode 489. 扫地机器人 - Harp Seal Pup Nursery and Caring Center

房间（用格栅表示）中有一个扫地机器人。格栅中的每一个格子有空和障碍物两种可能。

扫地机器人提供 4 个 API，可以向前进，向左转或者向右转。每次转弯 90 度。

当扫地机器人试图进入障碍物格子时，它的碰撞传感器会探测出障碍物，使它停留在原地。

请利用提供的 4 个 API 编写让机器人清理整个房间的算法。

interface Robot {
    // 若下一个方格为空，则返回true，并移动至该方格
    // 若下一个方格为障碍物，则返回false，并停留在原地
    boolean move();

    // 在调用turnLeft/turnRight后机器人会停留在原位置
    // 每次转弯90度
    void turnLeft();
    void turnRight();

    // 清理所在方格
    void clean();
}

示例:

输入:
room = [
  [1,1,1,1,1,0,1,1],
  [1,1,1,1,1,0,1,1],
  [1,0,1,1,1,1,1,1],
  [0,0,0,1,0,0,0,0],
  [1,1,1,1,1,1,1,1]
],
row = 1,
col = 3

解析:
房间格栅用0或1填充。0表示障碍物，1表示可以通过。
机器人从row=1，col=3的初始位置出发。在左上角的一行以下，三列以右。

注意:

输入只用于初始化房间和机器人的位置。你需要“盲解”这个问题。换而言之，你必须在对房间和机器人位置一无所知的情况下，只使用 4 个给出的 API 解决问题。
扫地机器人的初始位置一定是空地。
扫地机器人的初始方向向上。
所有可抵达的格子都是相连的，亦即所有标记为 1 的格子机器人都可以抵达。
可以假定格栅的四周都被墙包围。

题解

我们可以使用深度优先搜索来模拟机器人的扫地过程，即顺着当前机器人的朝向一直清扫下去，如果遇到障碍（清扫过的格子也算障碍），那么向右转向，直到找到一个没有障碍的朝向（继续进行搜索）或所有的朝向都有障碍（回溯）。

下图给出了机器人的扫地过程中某一步的状态，在此过程中，所有清扫过的格子都被视作障碍，不会重复经过。

bla

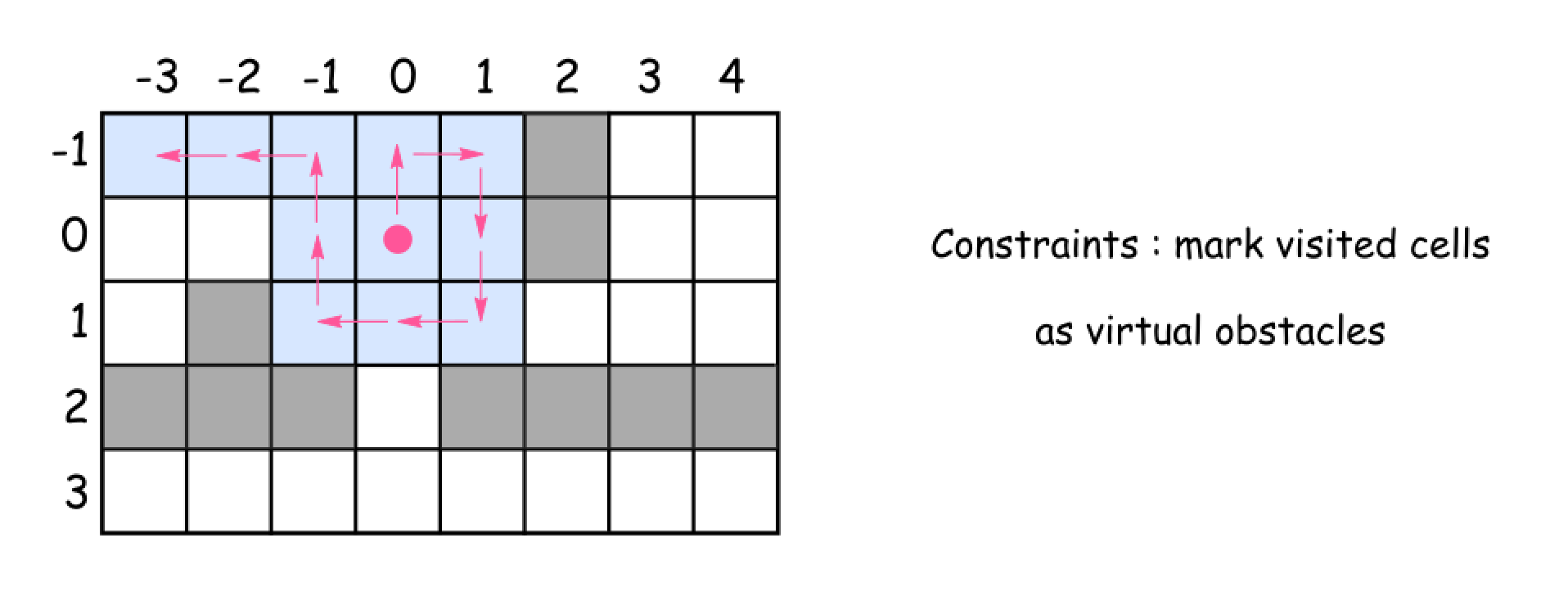
下图给出了机器人的回溯过程，在到达 (1, -3) 后，由于四个方向都是障碍，因此只能进行回溯，推到 (0, -3)。

bla

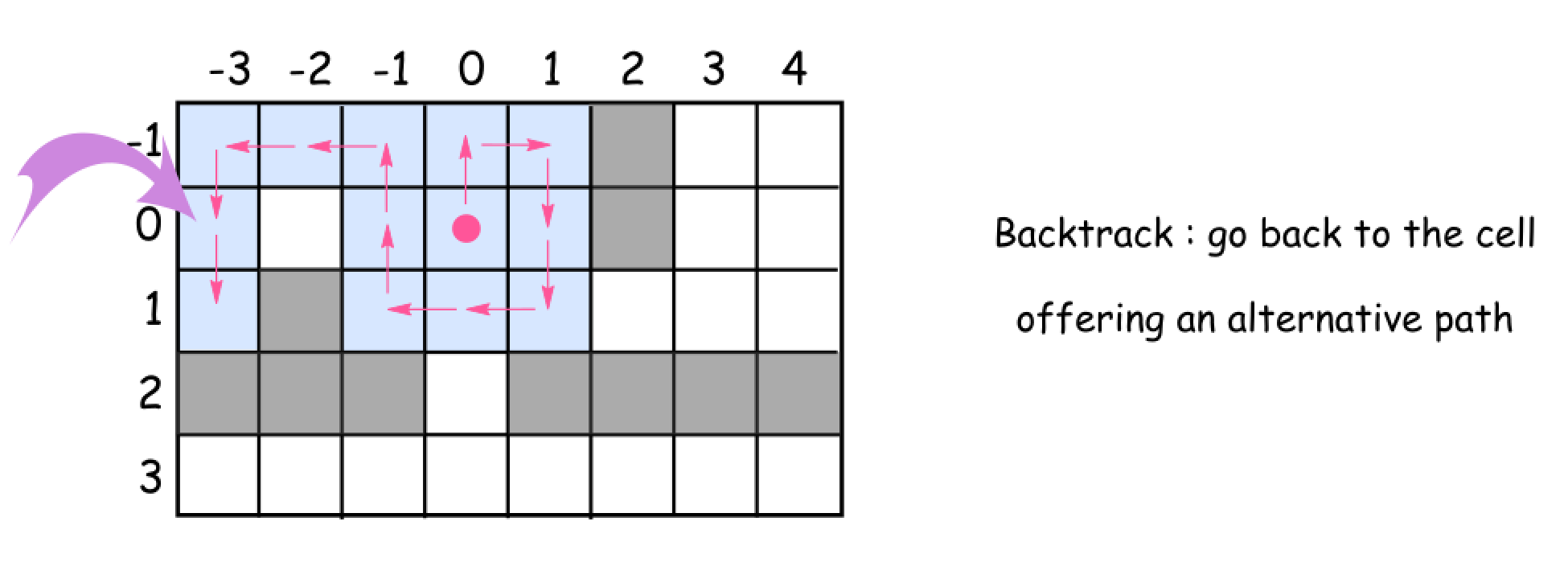
下面给出了整个算法的框架：

我们从起始位置开始，记录当前的位置为 cell = (0, 0)，以及机器人的朝向 direction = 0；
将起始位置进行清扫，并进行标记（即清扫过的格子也算作障碍）；
依次选择四个朝向 up，right，down 和 left 进行深度优先搜索，相邻的两个朝向仅差一次向右旋转的操作；
- 对于选择的朝向，检查下一个格子是否有障碍，如果没有，则向对应朝向移动一格，并开始新的搜索；
- 如果有，则向右旋转。
如果四个朝向都搜索完毕，则回溯到上一次搜索。

下图给出了根据此算法，机器人移动的过程。

bla

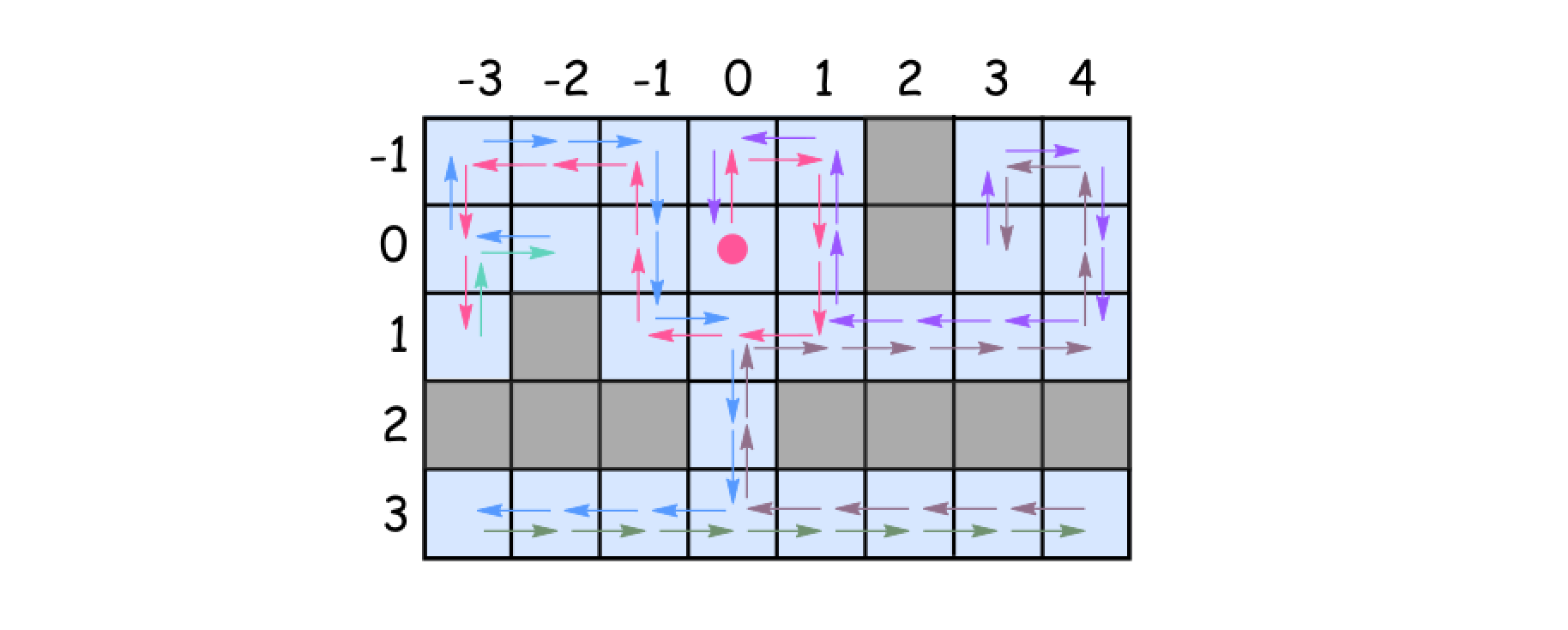
struct PairHash {   // 自定义hash函数
    size_t operator()(const pair<int, int>& key) const {
        return hash<int>{}(key.first * 131) ^ hash<int>{}(key.second);
    }
};
class Solution {
    int dirs[4][2] = {-1, 0, 0, 1, 1, 0, 0, -1};
    unordered_set<pair<int, int>, PairHash> vis;    // 防止重复访问
public:
    void cleanRoom(Robot& robot) {
        dfs(robot, 0, 0, 0);
    }

    void dfs(Robot& robot, int x, int y, int di) {
        vis.emplace(x, y);  // 标记为已访问
        robot.clean();
        for (int i = 0; i < 4; ++i) {
            int nd = (i + di) % 4, nx = x + dirs[nd][0], ny = y + dirs[nd][1];
            if (vis.count(make_pair(nx, ny)) == 0 && robot.move()) {
                dfs(robot, nx, ny, nd);

                // 回溯
                robot.turnRight();
                robot.turnRight();
                robot.move();   // 移动过的一步，再移动回来
                robot.turnRight();
                robot.turnRight();
            }
            robot.turnRight();
        }
    }
};

复杂度分析

时间复杂度：\(O(4^{N - M})\)，其中 \(N\) 是房间的大小，\(M\) 是障碍物的数量。
空间复杂度：\(O(N - M)\)。

azarasi / LeetCode 489. 扫地机器人

题解