Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中\(edges[i] = [type_i, u_i, v_i]\) 表示节点\(u_i\)和 \( v_i\) 之间存在类型为 \(type_i\) 的双向边。请你在保证图仍能够被 Alice 和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
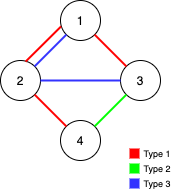
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2:
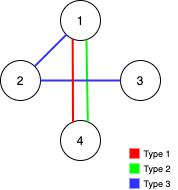
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3:
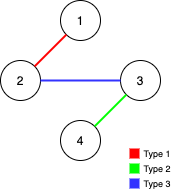
输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示:
- \(1 <= n <= 10^5\)
- \(1 <= edges.length <= min(10^5, 3 \times n \times (n-1) / 2)\)
edges[i].length == 31 <= edges[i][0] <= 31 <= edges[i][1] < edges[i][2] <= n- 所有元组 \((type_i, u_i, v_i)\) 互不相同
题解
思路与算法
我们称类型 \(1, 2, 3\) 的边分别为「Alice 独占边」「Bob 独占边」以及「公共边」。
首先我们需要思考什么样的图是可以被 Alice 和 Bob 完全遍历的。对于 Alice 而言,她可以经过的边是「Alice 独占边」以及「公共边」,由于她需要能够从任意节点到达任意节点,那么就说明:
当图中仅有「Alice 独占边」以及「公共边」时,整个图是连通的,即整个图只包含一个连通分量。
同理,对于 Bob 而言,当图中仅有「Bob 独占边」以及「公共边」时,整个图也要是连通的。
由于题目描述中希望我们删除最多数目的边,这等价于保留最少数目的边。换句话说,我们可以从一个仅包含 \(n\) 个节点(而没有边)的无向图开始,逐步添加边,使得满足上述的要求。
那么我们应该按照什么策略来添加边呢?直觉告诉我们,「公共边」的重要性大于「Alice 独占边」以及「Bob 独占边」,因为「公共边」是 Alice 和 Bob 都可以使用的,而他们各自的独占边却不能给对方使用。「公共边」的重要性也是可以证明的:
对于一条连接了两个不同的连通分量的「公共边」而言,如果我们不保留这条公共边,那么 Alice 和 Bob 就无法往返这两个连通分量,即他们分别需要使用各自的独占边。因此,Alice 需要一条连接这两个连通分量的独占边,Bob 同样也需要一条连接这两个连通分量的独占边,那么一共需要两条边,这就严格不优于直接使用一条连接这两个连通分量的「公共边」了。
因此,我们可以遵从优先添加「公共边」的策略。具体地,我们遍历每一条「公共边」,对于其连接的的两个节点:
如果这两个节点在同一个连通分量中,那么添加这条「公共边」是无意义的;
如果这两个节点不在同一个连通分量中,我们就可以(并且一定)添加这条「公共边」,然后合并这两个节点所在的连通分量。
这就提示了我们使用并查集来维护整个图的连通性,上述的策略只需要用到并查集的「查询」和「合并」这两个最基础的操作。
在处理完了所有的「公共边」之后,我们需要处理他们各自的独占边,而方法也与添加「公共边」类似。我们将当前的并查集复制一份,一份交给 Alice,一份交给 Bob。随后 Alice 不断地向并查集中添加「Alice 独占边」,Bob 不断地向并查集中添加「Bob 独占边」。在处理完了所有的独占边之后,如果这两个并查集都只包含一个连通分量,那么就说明 Alice 和 Bob 都可以遍历整个无向图。
细节
在使用并查集进行合并的过程中,我们每遇到一次失败的合并操作(即需要合并的两个点属于同一个连通分量),那么就说明当前这条边可以被删除,将答案增加 \(1\)。
代码
class Solution {
public int maxNumEdgesToRemove(int n, int[][] edges) {
UnionFind ufa = new UnionFind(n);
UnionFind ufb = new UnionFind(n);
int ans = 0;
// 节点编号改为从 0 开始
for (int[] edge : edges) {
--edge[1];
--edge[2];
}
// 公共边
for (int[] edge : edges) {
if (edge[0] == 3) {
if (!ufa.unite(edge[1], edge[2])) {
++ans;
} else {
ufb.unite(edge[1], edge[2]);
}
}
}
// 独占边
for (int[] edge : edges) {
if (edge[0] == 1) {
// Alice 独占边
if (!ufa.unite(edge[1], edge[2])) {
++ans;
}
} else if (edge[0] == 2) {
// Bob 独占边
if (!ufb.unite(edge[1], edge[2])) {
++ans;
}
}
}
if (ufa.setCount != 1 || ufb.setCount != 1) {
return -1;
}
return ans;
}
}
// 并查集模板
class UnionFind {
int[] parent;
int[] size;
int n;
// 当前连通分量数目
int setCount;
public UnionFind(int n) {
this.n = n;
this.setCount = n;
this.parent = new int[n];
this.size = new int[n];
Arrays.fill(size, 1);
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public boolean unite(int x, int y) {
x = findset(x);
y = findset(y);
if (x == y) {
return false;
}
if (size[x] < size[y]) {
int temp = x;
x = y;
y = temp;
}
parent[y] = x;
size[x] += size[y];
--setCount;
return true;
}
public boolean connected(int x, int y) {
x = findset(x);
y = findset(y);
return x == y;
}
}
复杂度分析
时间复杂度:\(O(m \cdot \alpha(n))\),其中 \(m\) 是数组 \(\textit{edges}\) 的长度,\(\alpha\) 是阿克曼函数的反函数。
空间复杂度:\(O(n)\),即为并查集需要使用的空间。