给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。
玩家 1 和玩家 2 轮流进行自己的回合,玩家 1 先手。开始时,两个玩家的初始分值都是 0。每一回合,玩家从数组的任意一端取一个数字(即,nums[0] 或nums[nums.length - 1]),取到的数字将会从数组中移除(数组长度减 1)。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时,游戏结束。
如果玩家 1 能成为赢家,返回 true 。如果两个玩家得分相等,同样认为玩家 1 是游戏的赢家,也返回 true。你可以假设每个玩家的玩法都会使他的分数最大化。
示例 1:
输入:nums = [1,5,2]
输出:false
解释:一开始,玩家 1 可以从 1 和 2 中进行选择。
如果他选择 2(或者 1 ),那么玩家 2 可以从 1(或者 2 )和 5 中进行选择。如果玩家 2 选择了 5 ,那么玩家 1 则只剩下 1(或者 2 )可选。
所以,玩家 1 的最终分数为 1 + 2 = 3,而玩家 2 为 5 。
因此,玩家 1 永远不会成为赢家,返回 false 。
示例 2:
输入:nums = [1,5,233,7]
输出:true
解释:玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个,玩家 1 都可以选择 233 。
最终,玩家 1(234 分)比玩家 2(12 分)获得更多的分数,所以返回 true,表示玩家 1 可以成为赢家。
提示:
1 <= nums.length <= 20- \(0 <= nums[i] <= 10^7\)
题解
方法一:递归
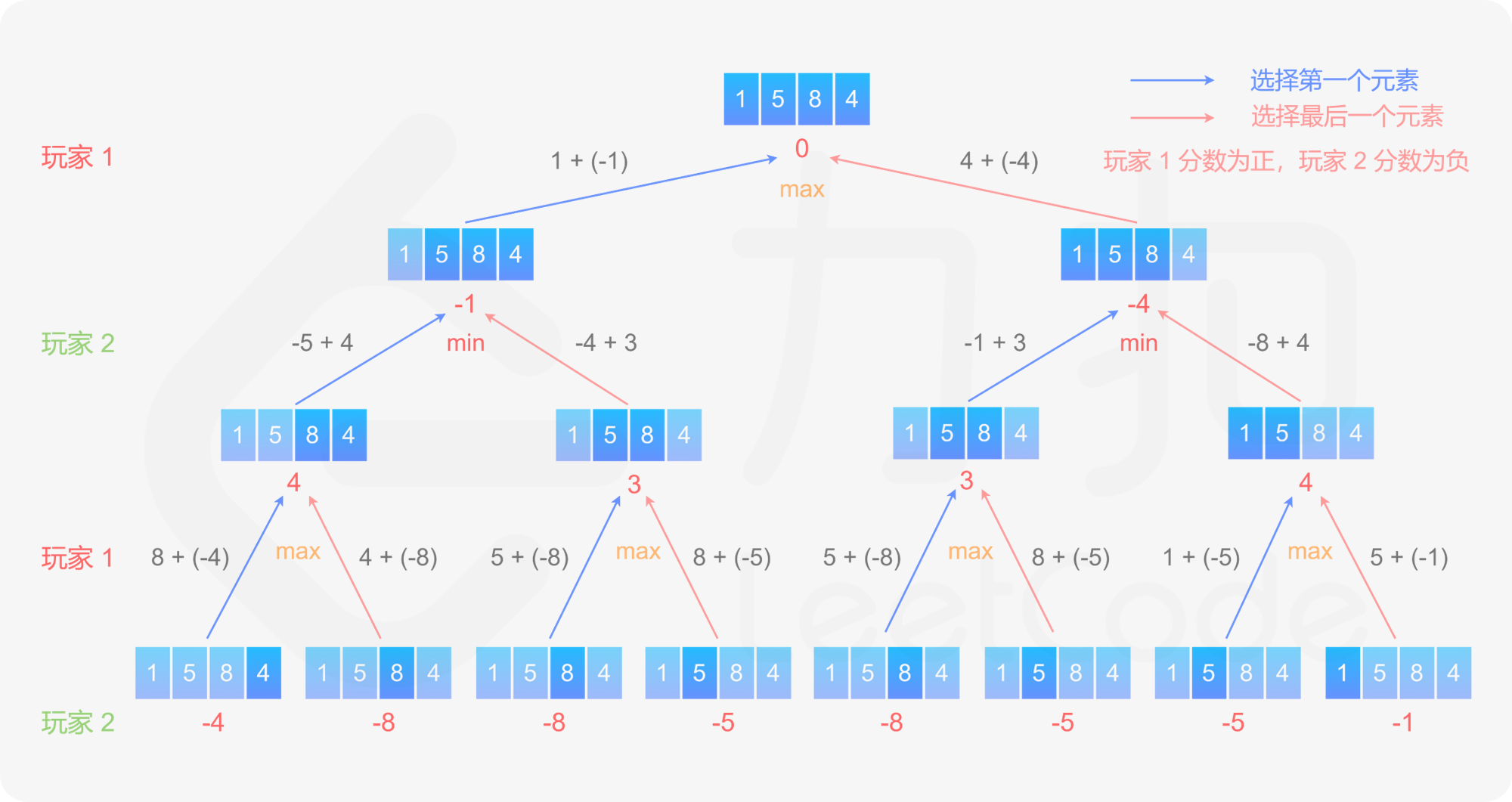
为了判断哪个玩家可以获胜,需要计算一个总分,即先手得分与后手得分之差。当数组中的所有数字都被拿取时,如果总分大于或等于 \(0\),则先手获胜,反之则后手获胜。
由于每次只能从数组的任意一端拿取数字,因此可以保证数组中剩下的部分一定是连续的。假设数组当前剩下的部分为下标 \(\textit{start}\) 到下标 \(\textit{end}\),其中 \(0 \le \textit{start} \le \textit{end} < \textit{nums}.\text{length}\)。如果 \(\textit{start}=\textit{end}\),则只剩一个数字,当前玩家只能拿取这个数字。如果 \(\textit{start}<\textit{end}\),则当前玩家可以选择 \(\textit{nums}[\textit{start}]\) 或 \(\textit{nums}[\textit{end}]\),然后轮到另一个玩家在数组剩下的部分选取数字。这是一个递归的过程。
计算总分时,需要记录当前玩家是先手还是后手,判断当前玩家的得分应该记为正还是负。当数组中剩下的数字多于 \(1\) 个时,当前玩家会选择最优的方案,使得自己的分数最大化,因此对两种方案分别计算当前玩家可以得到的分数,其中的最大值为当前玩家最多可以得到的分数。
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
return total(nums, 0, nums.size() - 1, 1) >= 0;
}
int total(vector<int>& nums, int start, int end, int turn) {
if (start == end) {
return nums[start] * turn;
}
int scoreStart = nums[start] * turn + total(nums, start + 1, end, -turn);
int scoreEnd = nums[end] * turn + total(nums, start, end - 1, -turn);
return max(scoreStart * turn, scoreEnd * turn) * turn;
}
};
复杂度分析
时间复杂度:\(O(2^n)\),其中 \(n\) 是数组的长度。
空间复杂度:\(O(n)\),其中 \(n\) 是数组的长度。空间复杂度取决于递归使用的栈空间。
方法二:动态规划
方法一使用递归,存在大量重复计算,因此时间复杂度很高。由于存在重复子问题,因此可以使用动态规划降低时间复杂度。
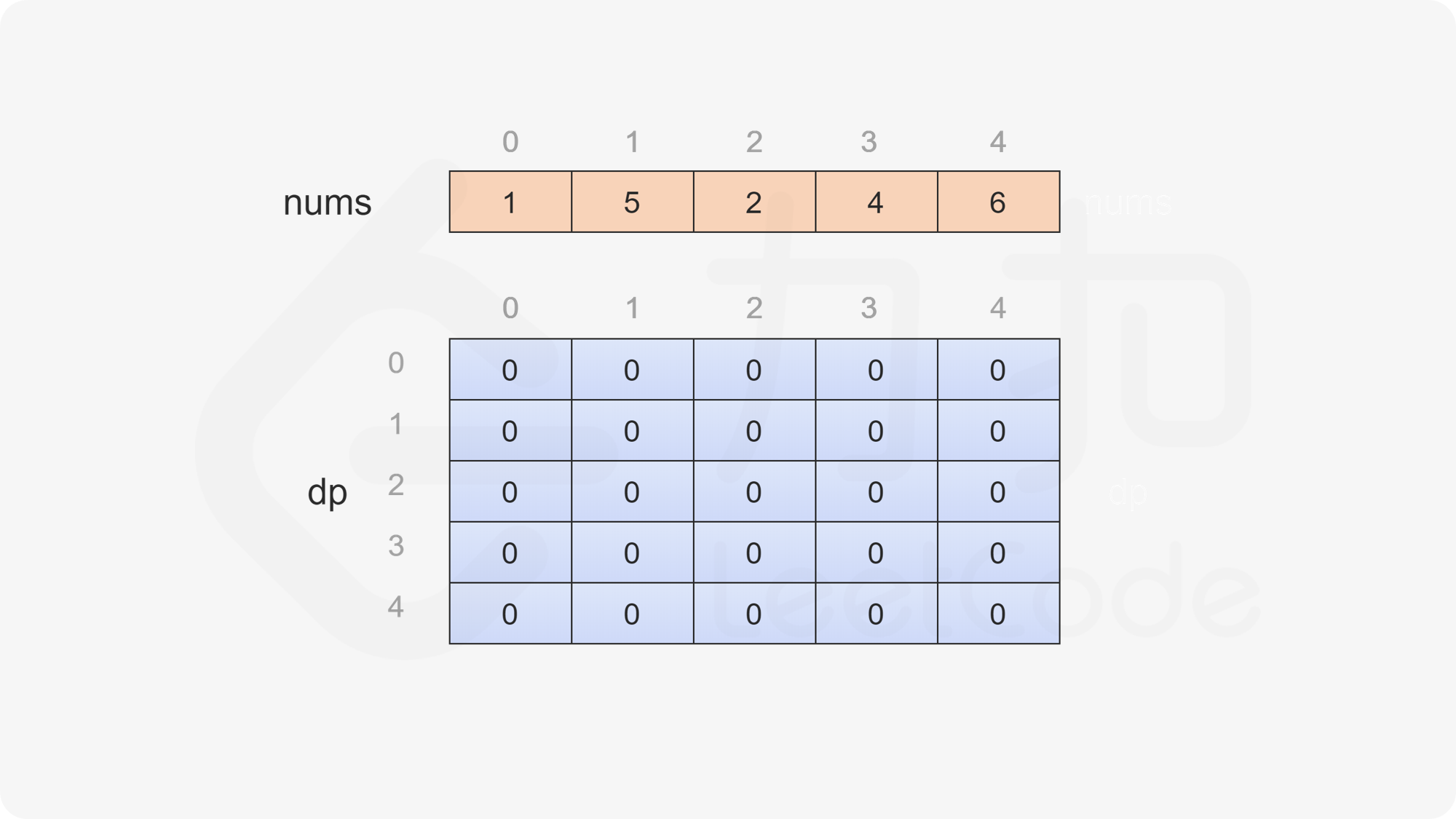
定义二维数组 \(\textit{dp}\),其行数和列数都等于数组的长度,\(\textit{dp}[i][j]\) 表示当数组剩下的部分为下标 \(i\) 到下标 \(j\) 时,即在下标范围 \([i, j]\) 中,当前玩家与另一个玩家的分数之差的最大值,注意当前玩家不一定是先手。
只有当 \(i \le j\) 时,数组剩下的部分才有意义,因此当 \(i>j\) 时,\(\textit{dp}[i][j]=0\)。
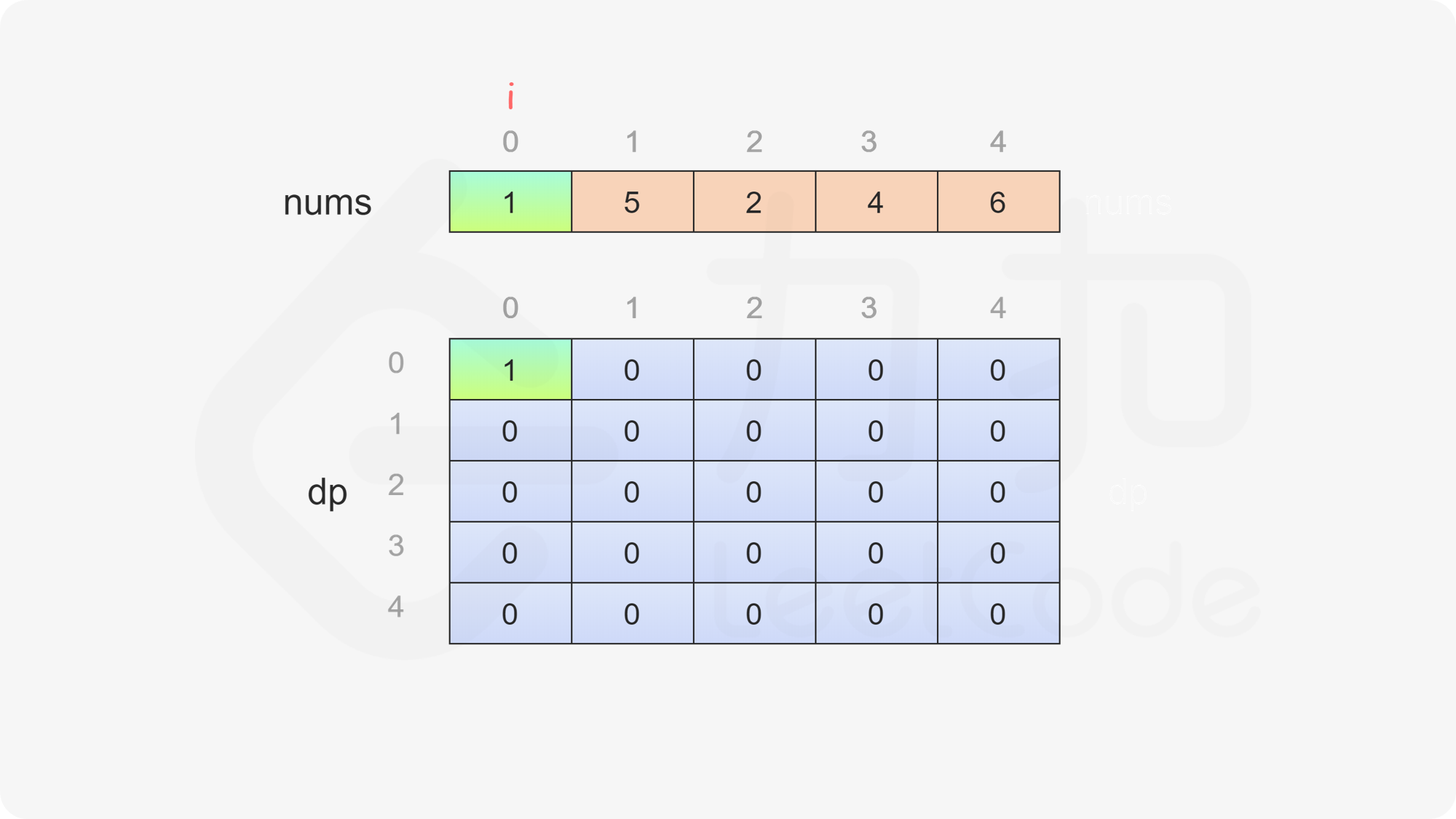
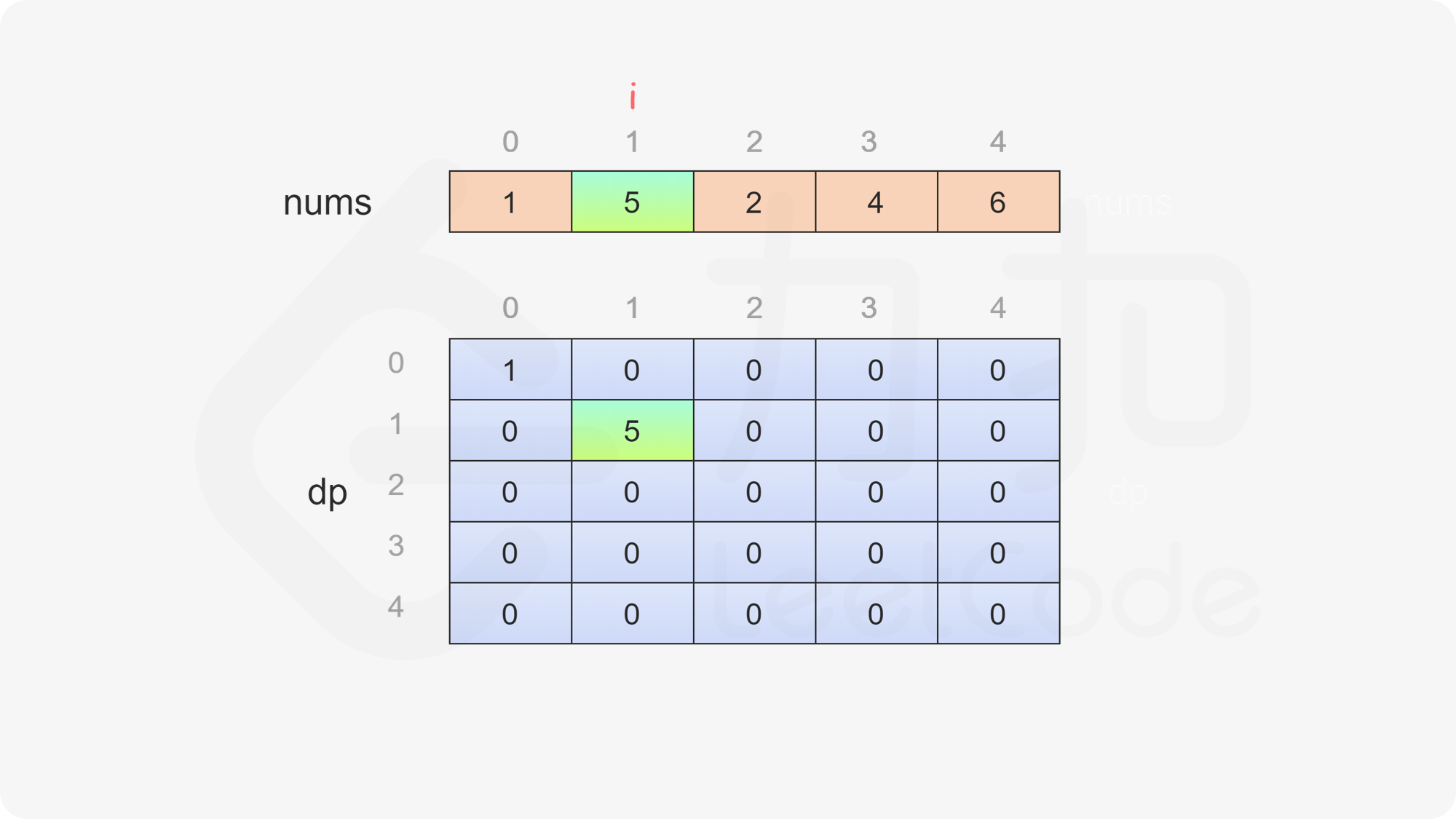
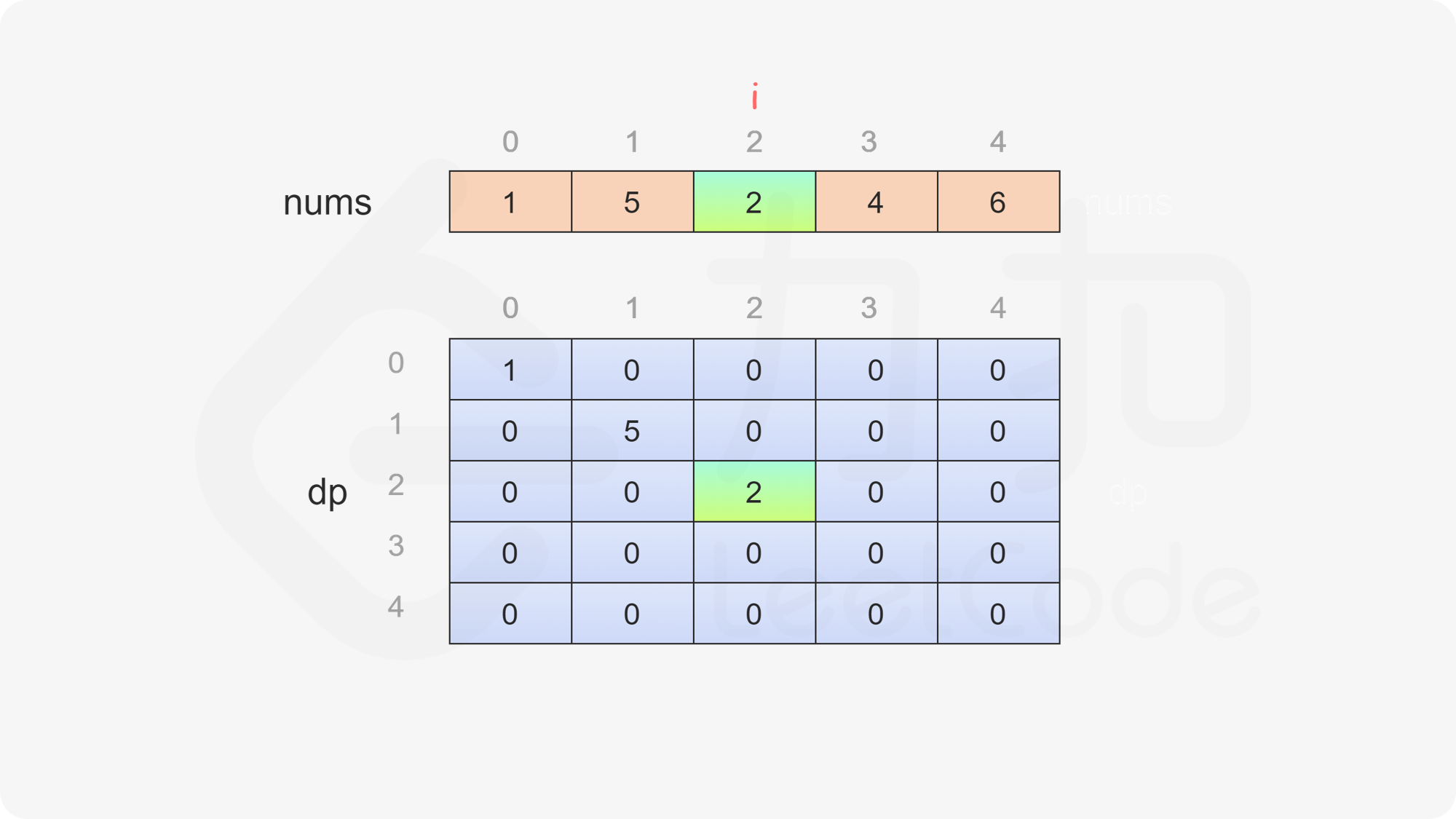
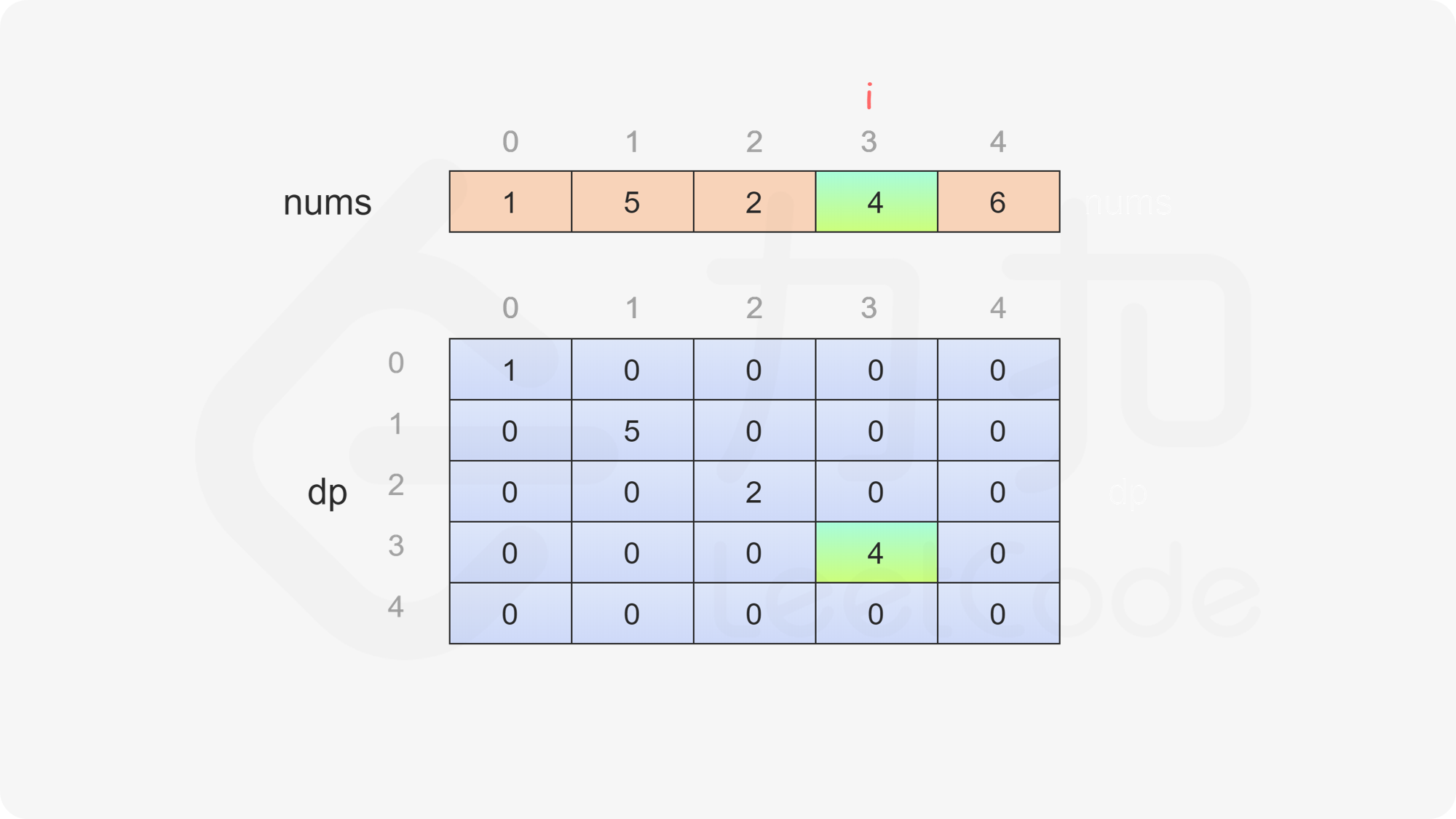
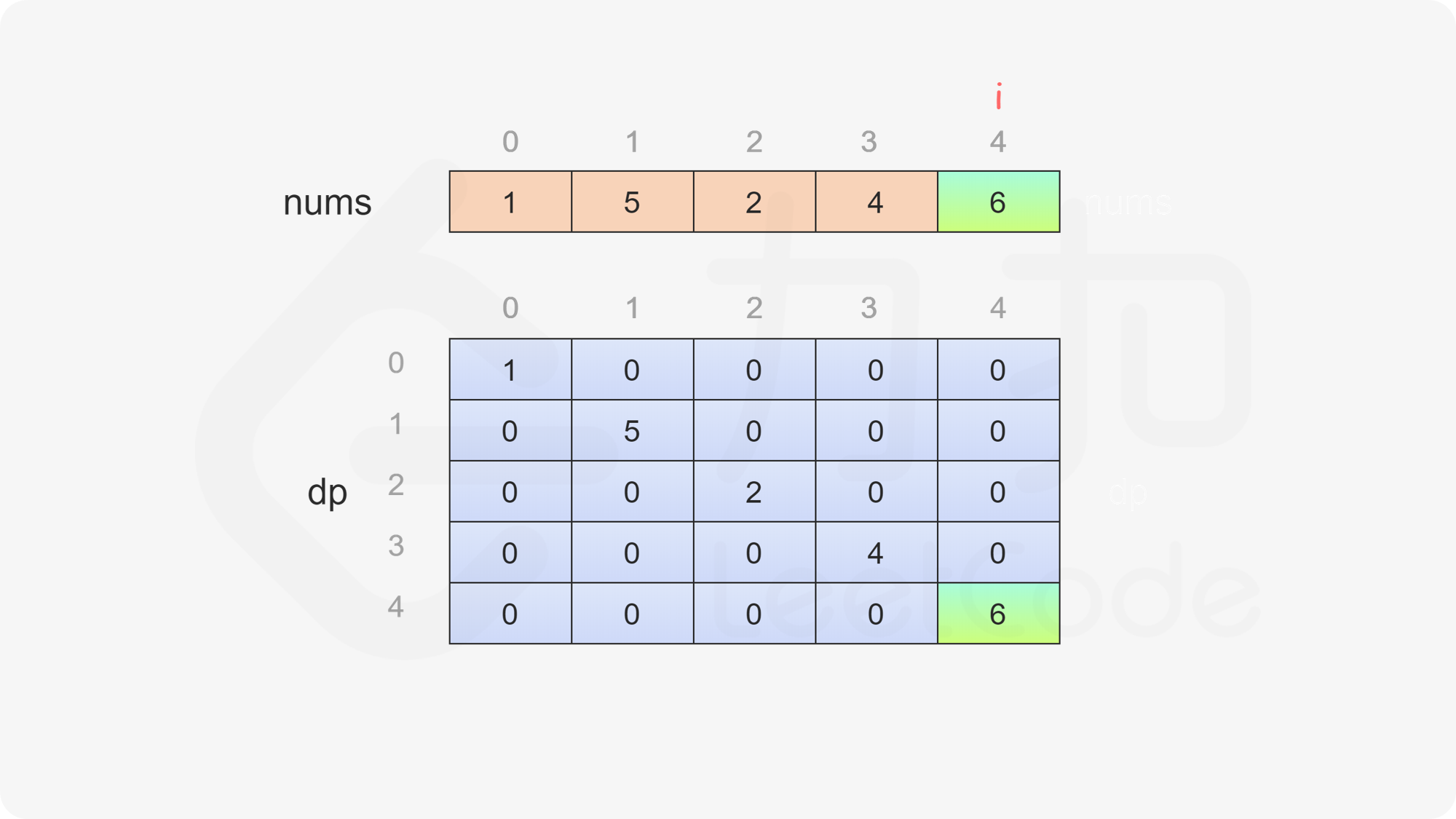
当 \(i=j\) 时,只剩一个数字,当前玩家只能拿取这个数字,因此对于所有 \(0 \le i < \textit{nums}.\text{length}\),都有 \(\textit{dp}[i][i]=\textit{nums}[i]\)。
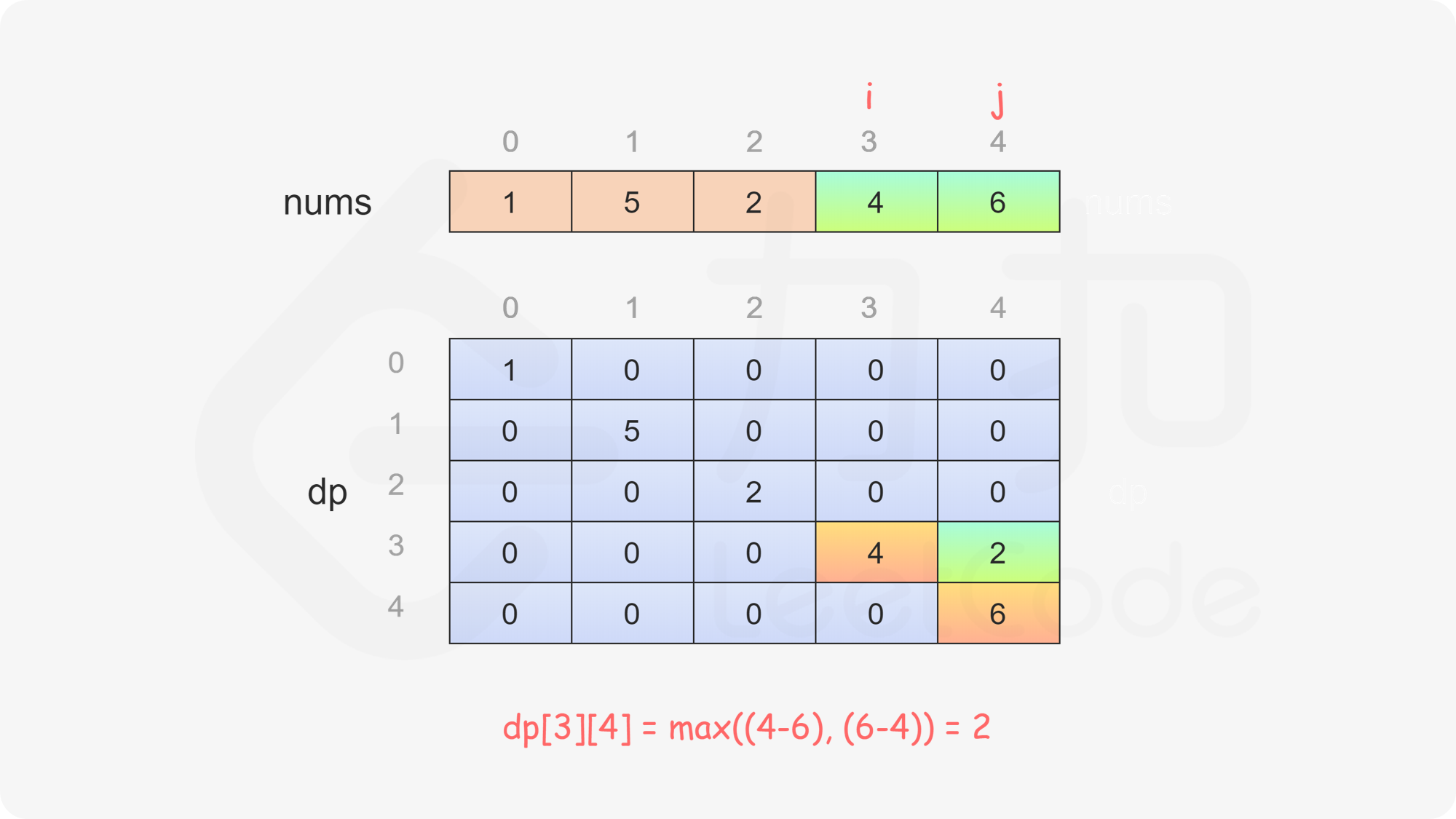
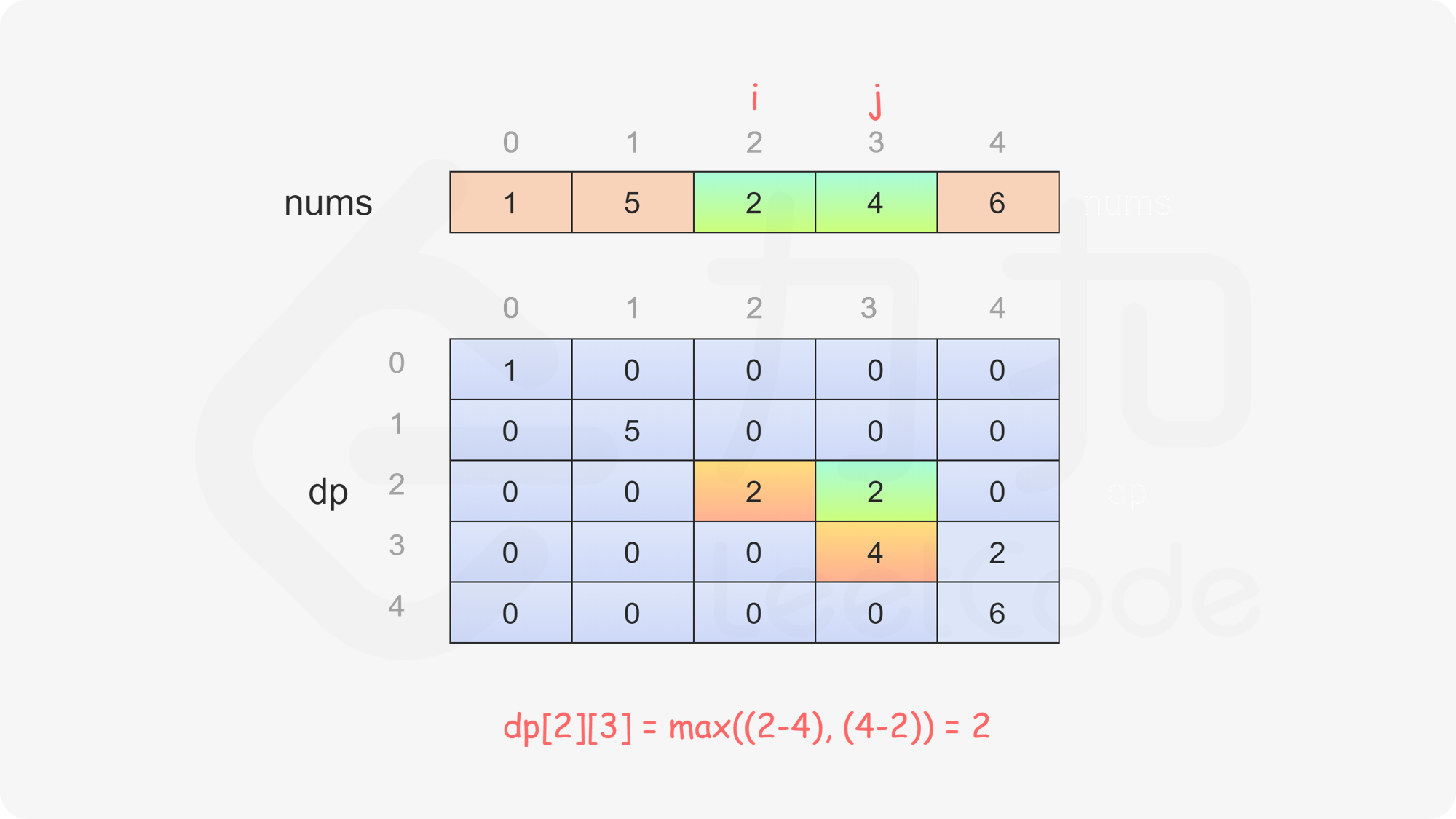
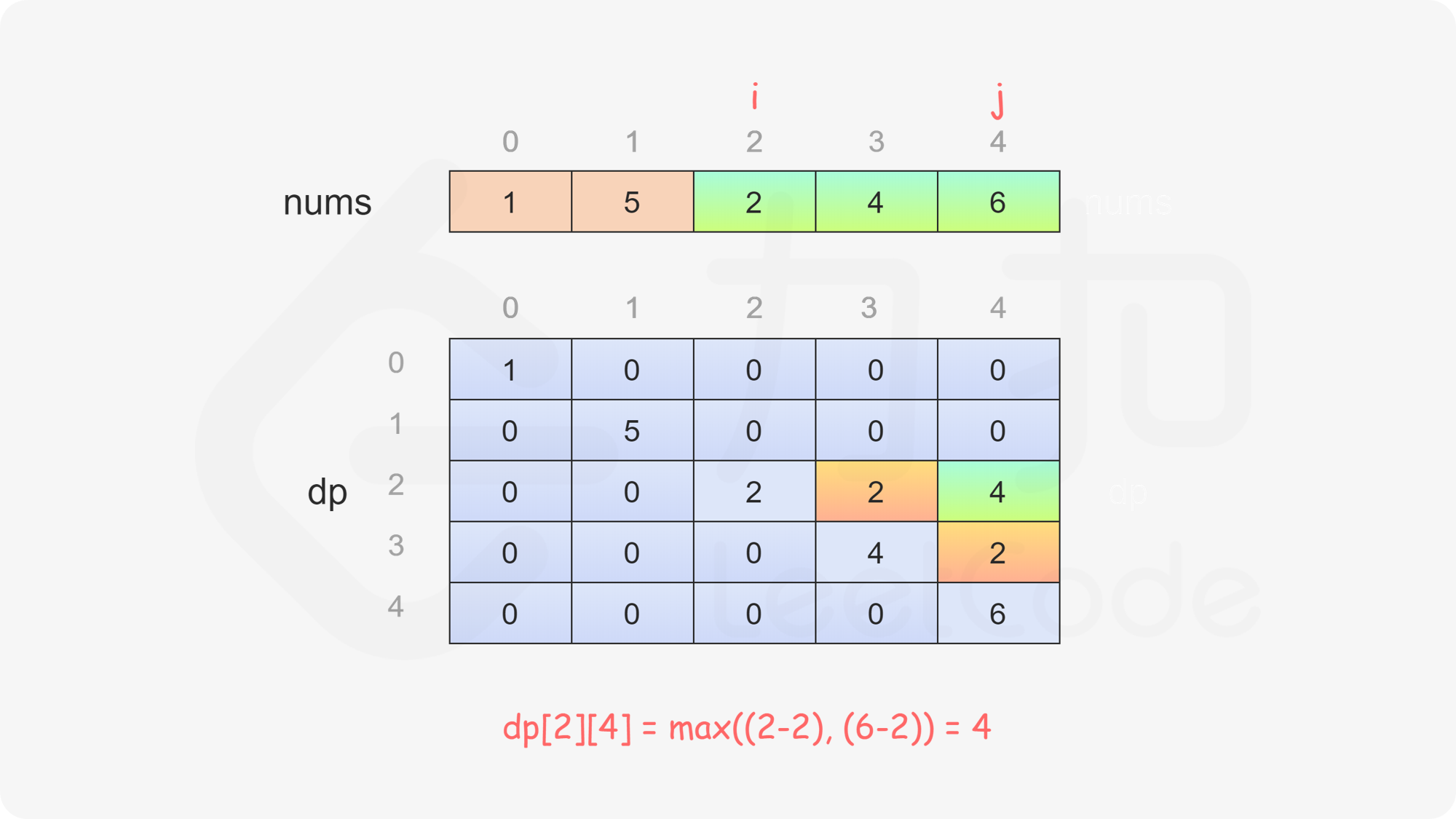
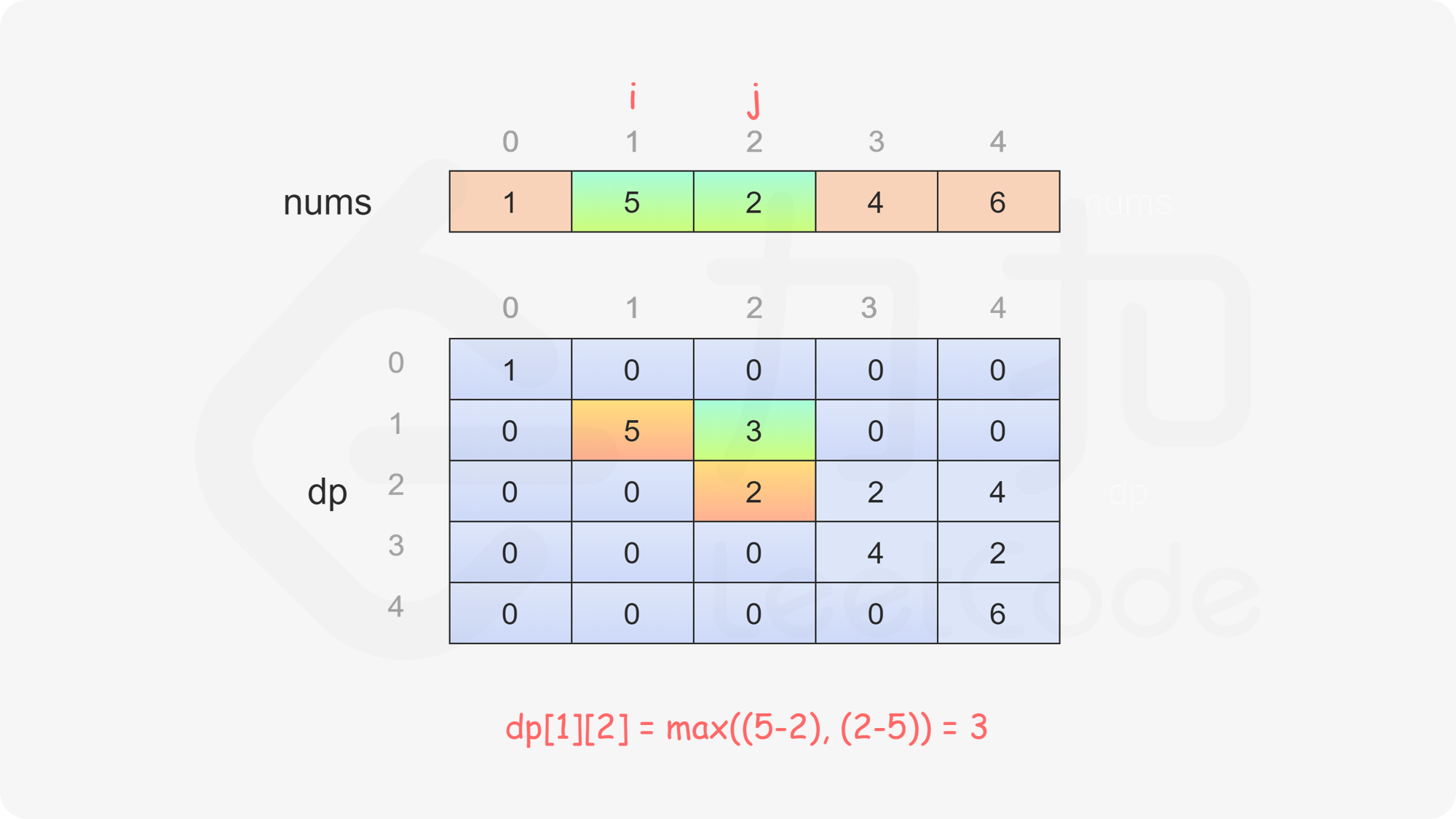
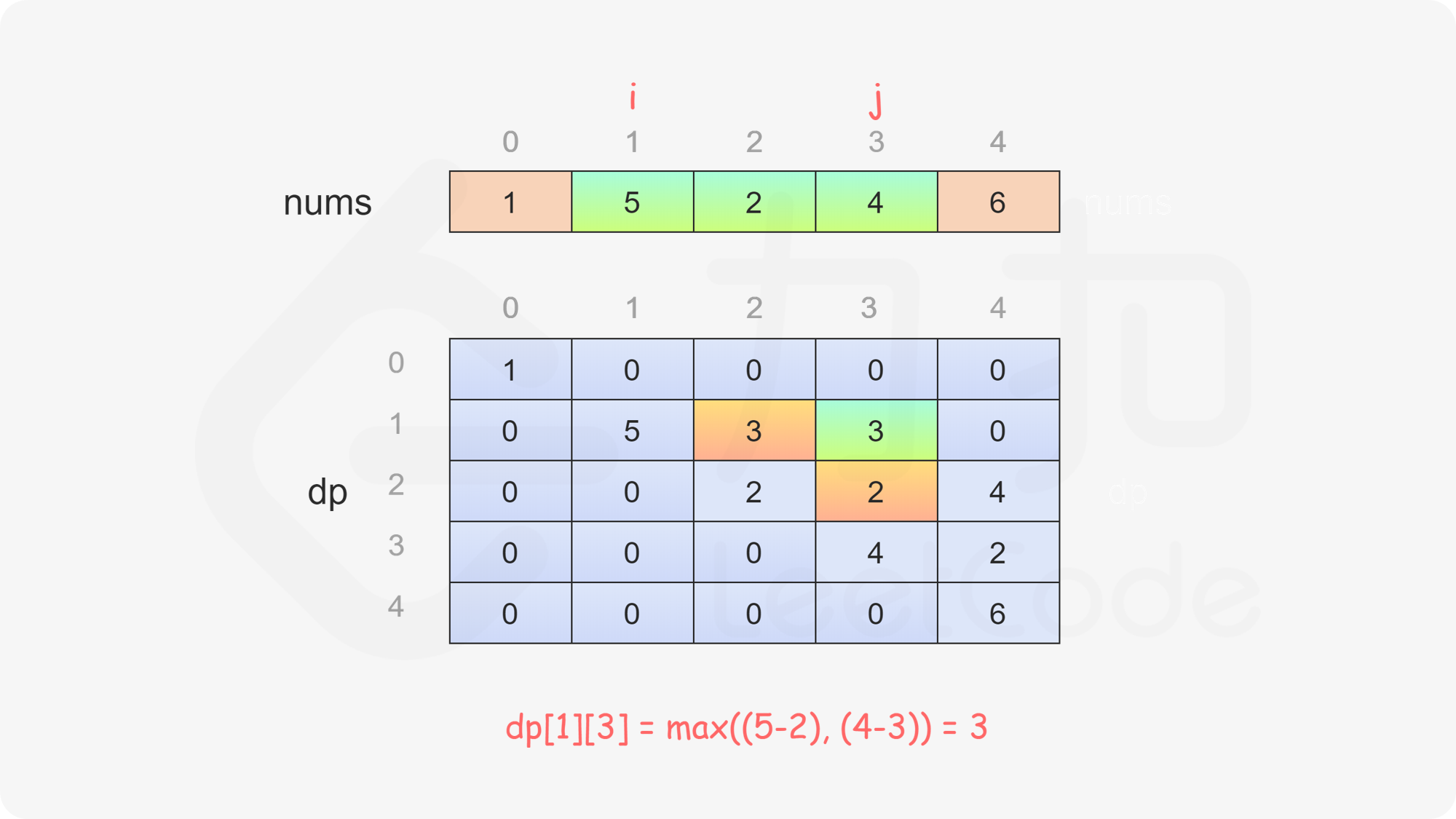
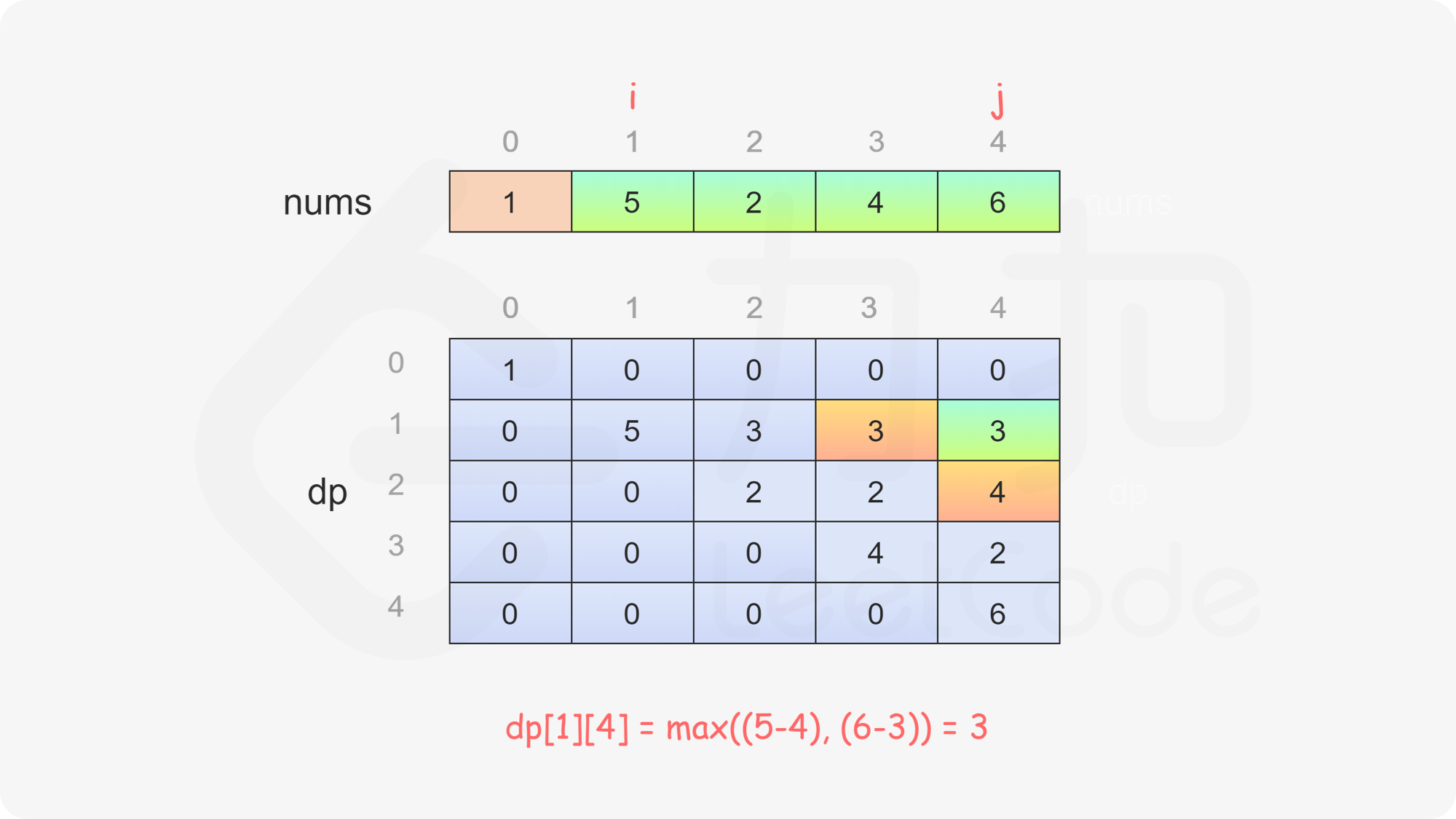
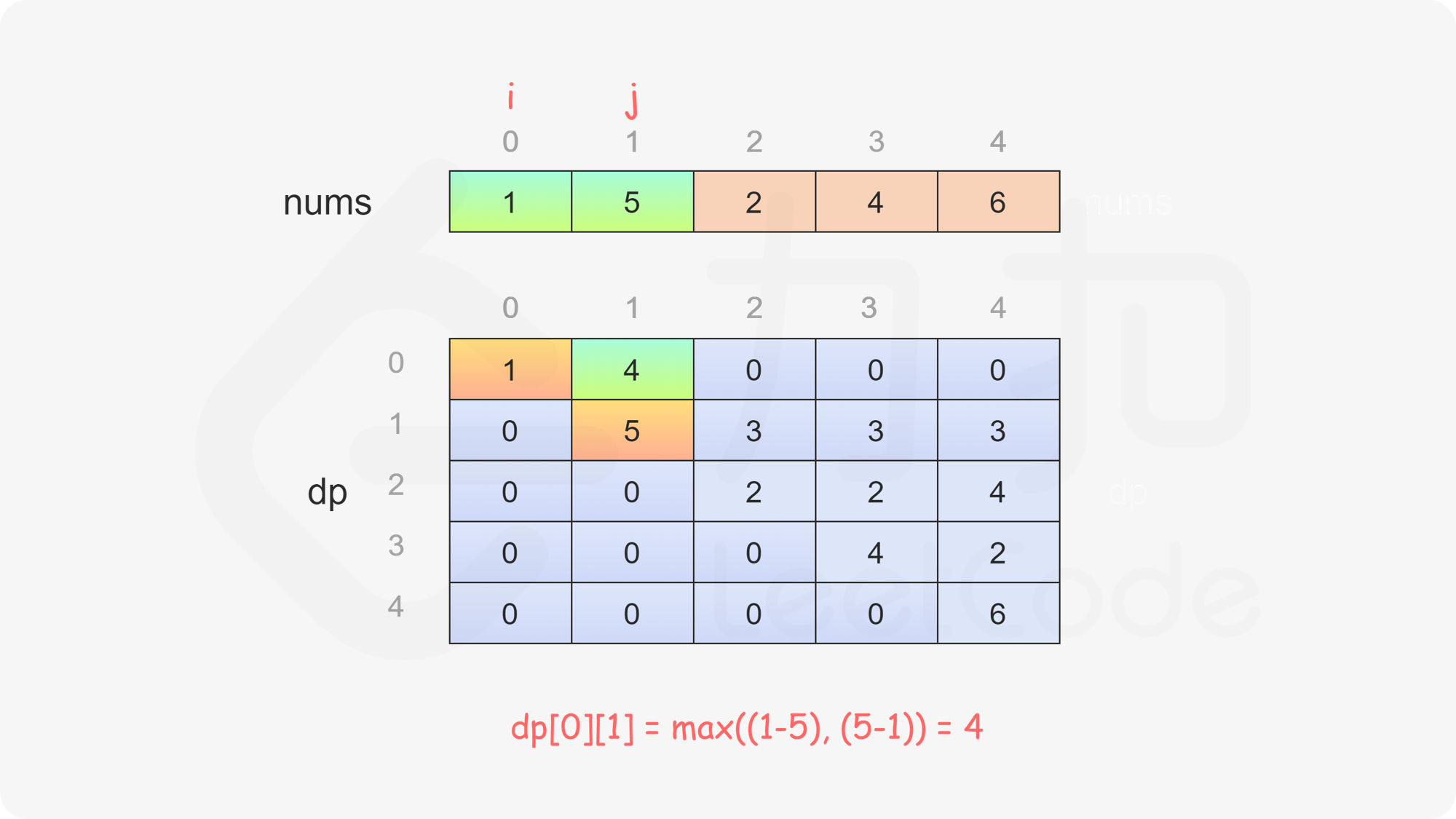
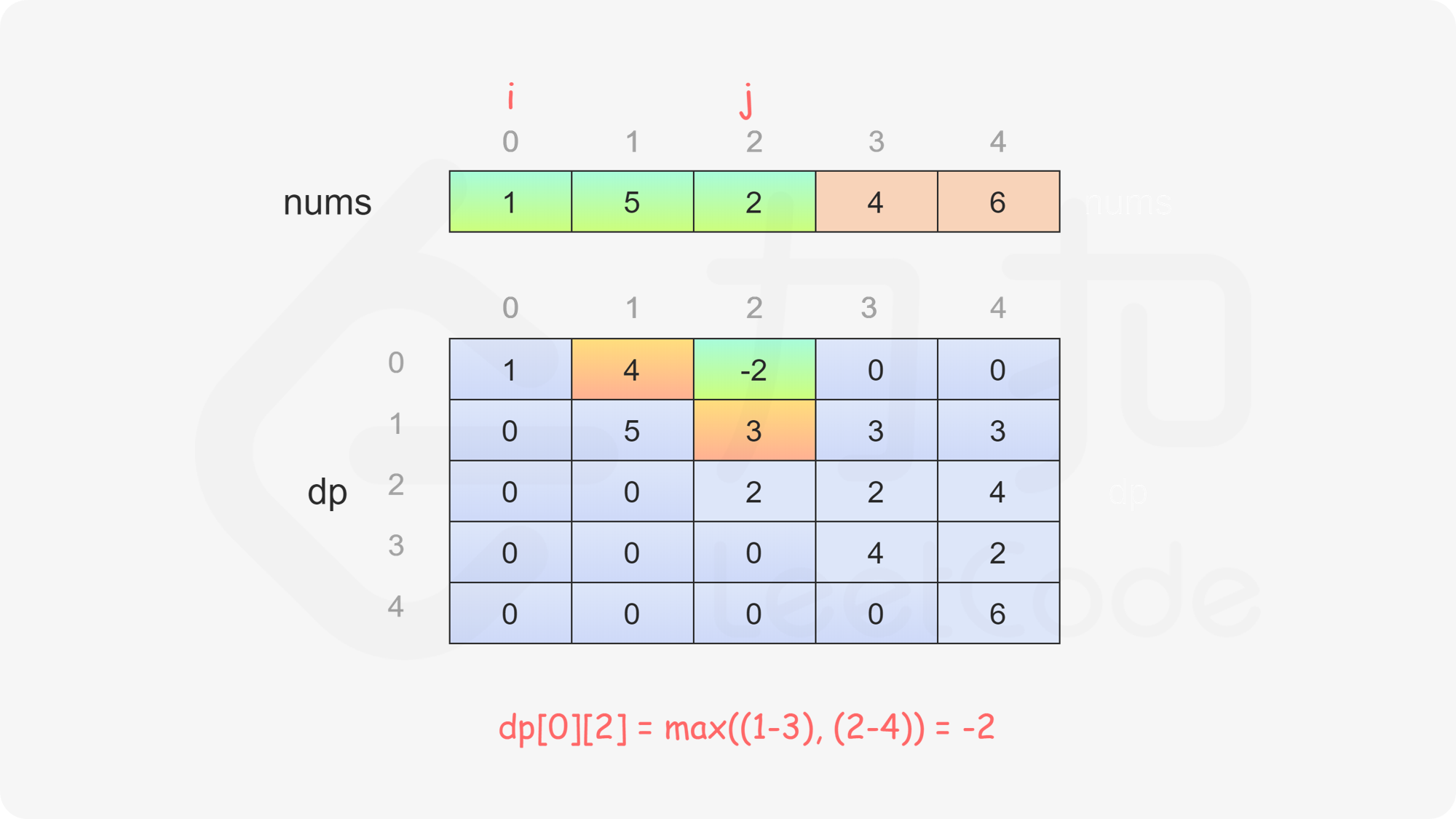
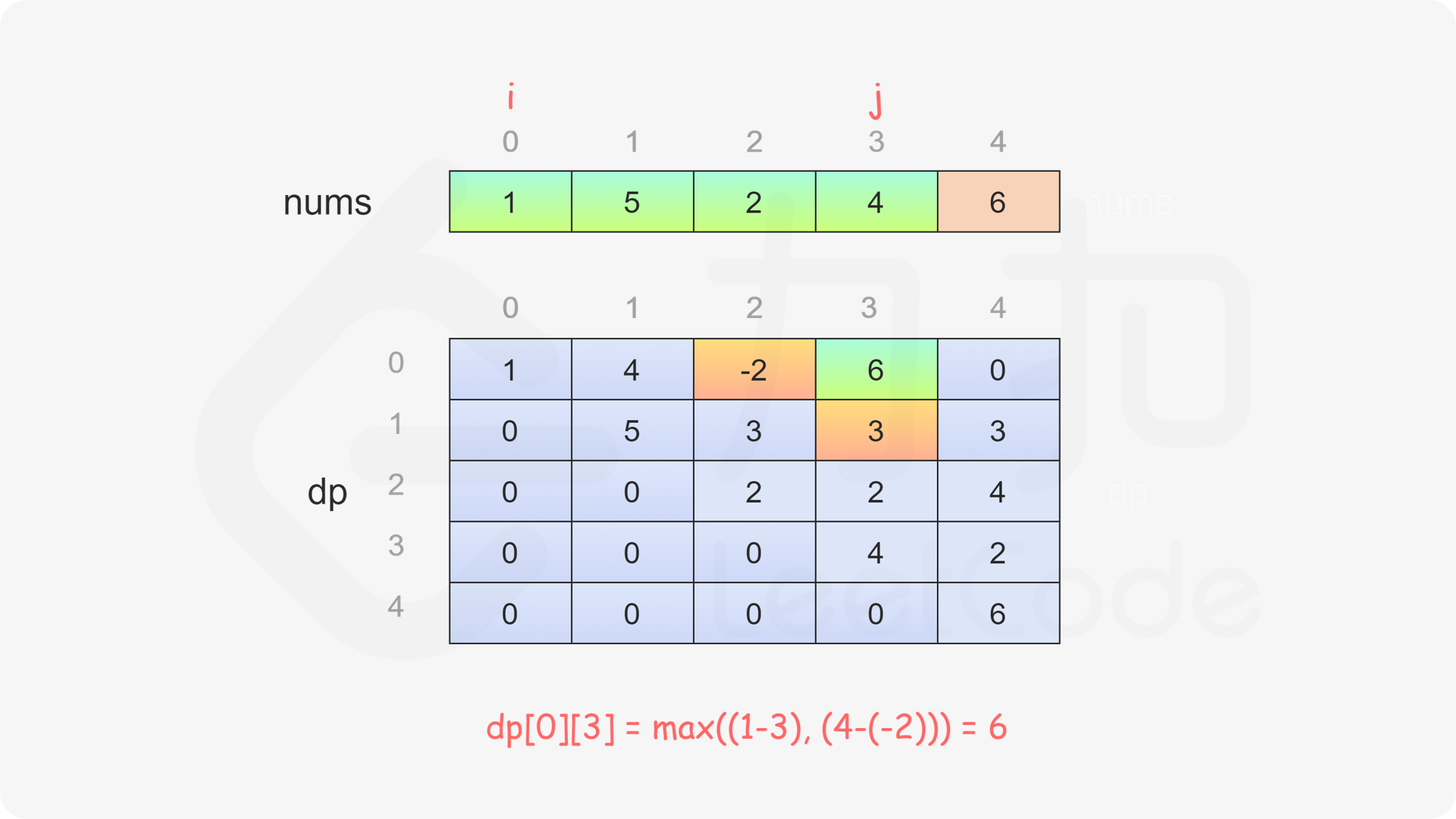
当 \(i<j\) 时,当前玩家可以选择 \(\textit{nums}[i]\) 或 \(\textit{nums}[j]\),然后轮到另一个玩家在数组剩下的部分选取数字。在两种方案中,当前玩家会选择最优的方案,使得自己的分数最大化。因此可以得到如下状态转移方程:
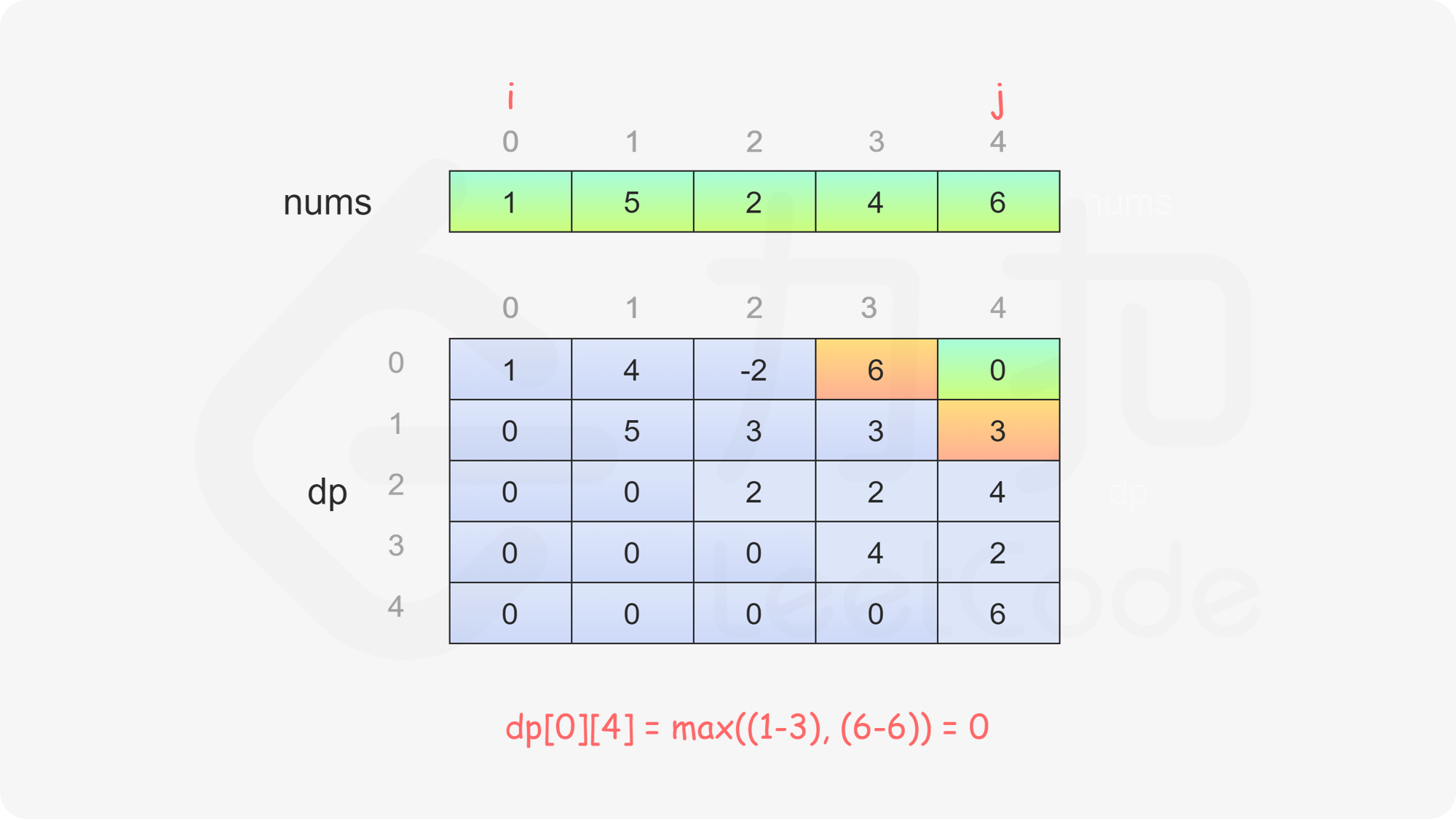
$$ \textit{dp}[i][j]=\max(\textit{nums}[i] - \textit{dp}[i + 1][j], \textit{nums}[j] - \textit{dp}[i][j - 1]) $$
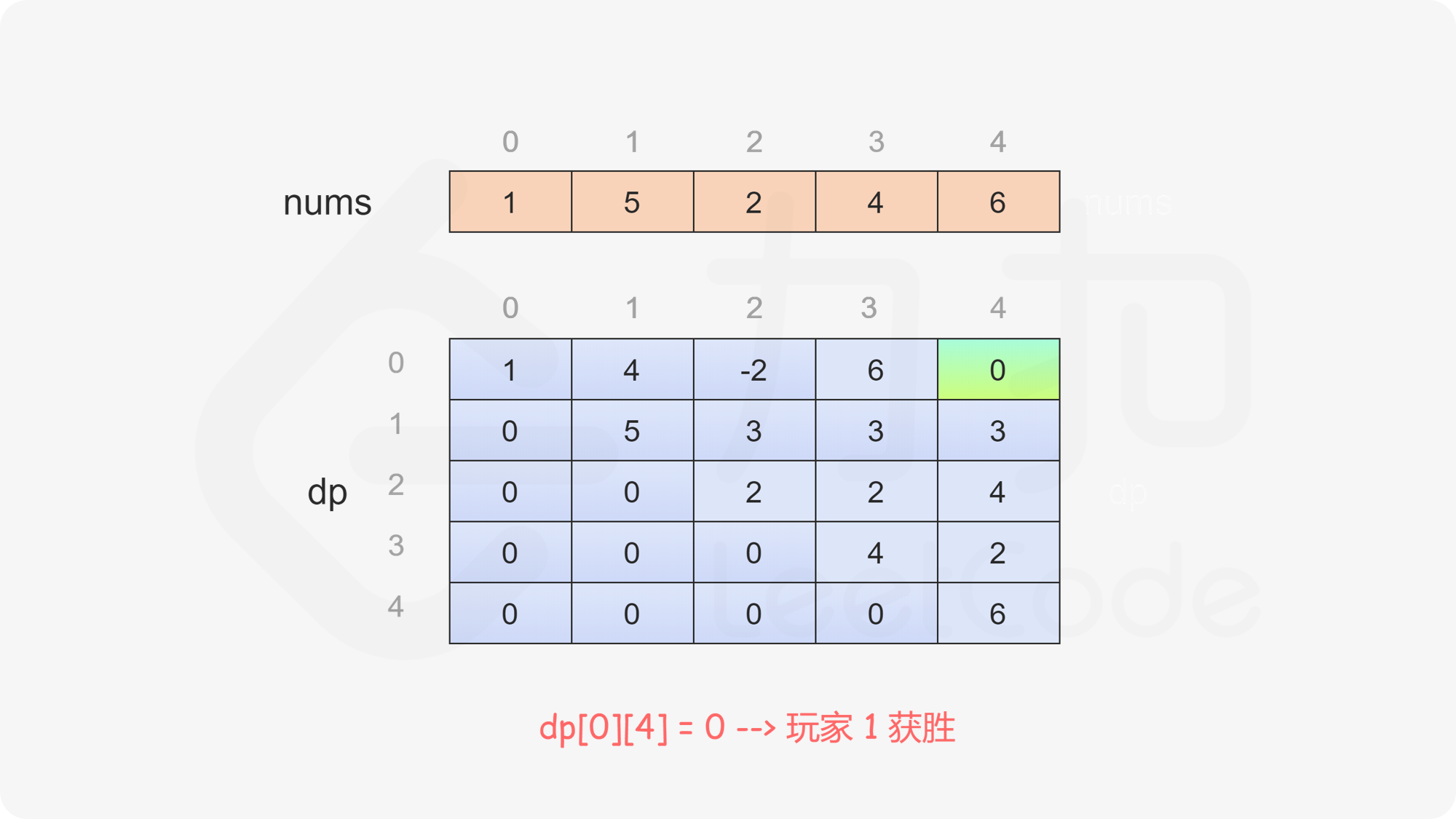
最后判断 \(\textit{dp}[0][\textit{nums}.\text{length}-1]\) 的值,如果大于或等于 \(0\),则先手得分大于或等于后手得分,因此先手成为赢家,否则后手成为赢家。
 >
>
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
int length = nums.size();
auto dp = vector<vector<int>> (length, vector<int>(length));
for (int i = 0; i < length; i++) {
dp[i][i] = nums[i];
}
for (int i = length - 2; i >= 0; i--) {
for (int j = i + 1; j < length; j++) {
dp[i][j] = max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1]);
}
}
return dp[0][length - 1] >= 0;
}
};
上述代码中使用了二维数组 \(\textit{dp}\)。分析状态转移方程可以看到,\(\textit{dp}[i][j]\) 的值只和 \(\textit{dp}[i + 1][j]\) 与 \(\textit{dp}[i][j - 1]\) 有关,即在计算 \(\textit{dp}\) 的第 \(i\) 行的值时,只需要使用到 \(\textit{dp}\) 的第 \(i\) 行和第 \(i+1\) 行的值,因此可以使用一维数组代替二维数组,对空间进行优化。
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
int length = nums.size();
auto dp = vector<int>(length);
for (int i = 0; i < length; i++) {
dp[i] = nums[i];
}
for (int i = length - 2; i >= 0; i--) {
for (int j = i + 1; j < length; j++) {
dp[j] = max(nums[i] - dp[j], nums[j] - dp[j - 1]);
}
}
return dp[length - 1] >= 0;
}
};
复杂度分析
时间复杂度:\(O(n^2)\),其中 \(n\) 是数组的长度。需要计算每个子数组对应的 \(\textit{dp}\) 的值,共有 \(\frac{n(n+1)}{2}\) 个子数组。
空间复杂度:\(O(n)\),其中 \(n\) 是数组的长度。空间复杂度取决于额外创建的数组 \(\textit{dp}\),如果不优化空间,则空间复杂度是 \(O(n^2)\),使用一维数组优化之后空间复杂度可以降至 \(O(n)\)。