You are given an array pairs, where \(pairs[i] = [x_i, y_i]\), and:
- There are no duplicates.
- \(x_i < y_i\)
Let ways be the number of rooted trees that satisfy the following conditions:
- The tree consists of nodes whose values appeared in
pairs. - A pair \([x_i, y_i]\) exists in
pairsif and only if \(x_i\) is an ancestor of \(y_i\) or \(y_i\) is an ancestor of \(x_i\). - Note: the tree does not have to be a binary tree.
Two ways are considered to be different if there is at least one node that has different parents in both ways.
Return:
0ifways == 01ifways == 12ifways > 1
A rooted tree is a tree that has a single root node, and all edges are oriented to be outgoing from the root.
An ancestor of a node is any node on the path from the root to that node (excluding the node itself). The root has no ancestors.
Example 1:
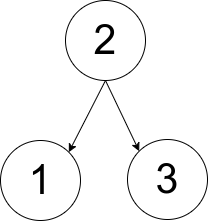
Input: pairs = [[1,2],[2,3]]
Output: 1
Explanation: There is exactly one valid rooted tree, which is shown in the above figure.
Example 2:

Input: pairs = [[1,2],[2,3],[1,3]]
Output: 2
Explanation: There are multiple valid rooted trees. Three of them are shown in the above figures.
Example 3:
Input: pairs = [[1,2],[2,3],[2,4],[1,5]]
Output: 0
Explanation: There are no valid rooted trees.
Constraints:
- \(1 <= pairs.length <= 10^5\)
- \(1 <= x_i < y_i <= 500\)
- The elements in
pairsare unique. - Think inductively. The first step is to get the root. Obviously, the root should be in pairs with all the nodes. If there isn’t exactly one such node, then there are 0 ways.
- The number of pairs involving a node must be less than or equal to that number of its parent.
- Actually, if it’s equal, then there is not exactly 1 way, because they can be swapped.
- Recursively, given a set of nodes, get the node with the most pairs, then this must be a root and have no parents in the current set of nodes.
Solution
本题抽象思维难度较大,需要仔细考虑树的结构。题目给定的数对 \(\textit{pairs}[i] = [x_{i},y_{i}]\),且满足 \(x_i\) 是 \(y_i\) 的祖先或者 \(y_i\) 是 \(x_i\) 的祖先;树中所包含的所有节点值都在 pairs 中,即 pairs 包含树中所有可能构成祖先的数对。
设树中节点数目为 n,pairs 中包含节点 x 的数对的数目为 degree[x],节点 x 的祖先和后代的节点集合为 adj[x]。
下面来研究 degree 的性质。
- 根节点为树中其余所有节点的祖先,根节点与其余所有节点都能构成数对。设根节点为 root,由于 pairs 包含树中所有可能构成祖先的数对,因此 degree[root]=n−1。如下图所示,根节点 1 为其余节点的祖先,蓝色节点组成了 adj[1]。
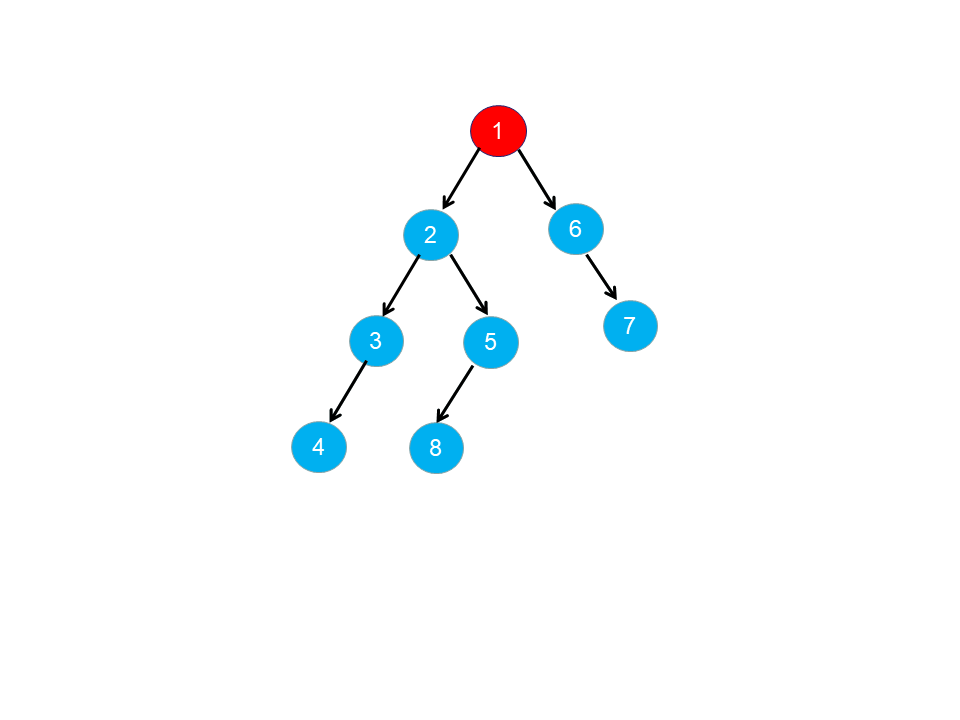
- 对于 pairs 中的数对 \([x_i,y_i]\),如果 \(x_i\) 为 \(y_i\) 的祖先,则一定满足 \(degree[x_i]≥degree[y_i]\)。如果节点 \(y_j\) 为节点 \(y_i\) 的后代节点,则节点 \(y_j\) 一定同时也是节点 \(x_i\) 的后代节点;如果节点 \(y_j\) 为节点 \(y_i\) 的祖先节点,则节点 \(y_j\) 要么是节点 \(x_i\) 的祖先节点,要么是节点 \(x_i\) 的后代节点,所以一定满足 \(degree[x_i]≥degree[y_i]\)。此外,如果 \(x_i\) 为 \(y_i\) 的祖先,则一定满足 \(adj[y_i]∈adj[x_i]\)。如下图所示,含有节点 2 的数对数目一定大于含有节点 3 的数对数目。
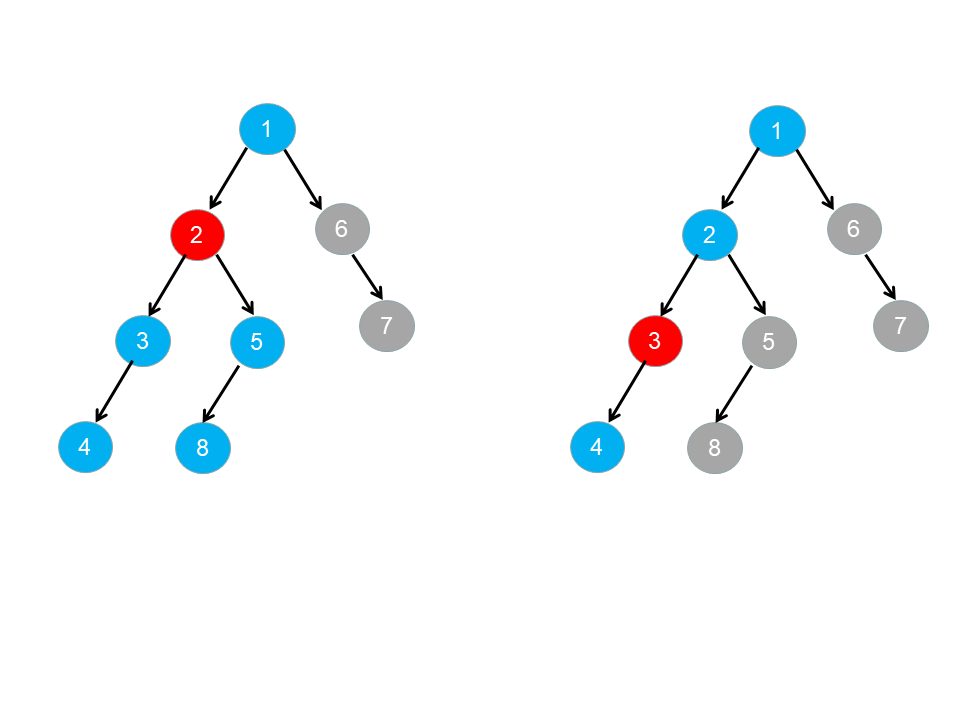
- 对于 pairs 中的数对 \([x_i,y_i]\),如果 \(x_i\) 为 \(y_i\) 的祖先,且满足 \(degree[x_i]=degree[y_i]\) 和 \(adj[x_i]=adj[y_i]\),则 \(x_i\) 到 \(y_i\) 途径的所有节点均只有一个孩子节点。此时 \(x_i\) 到 \(y_i\) 之间的节点包含的数对关系是一样的,\(x_i\) 到 \(y_i\) 之间的节点是可以进行互相交换而不影响树的结构,则此时构成树的方案数一定不是唯一的。如下图所示,节点 6,7,9 满足上述要求:
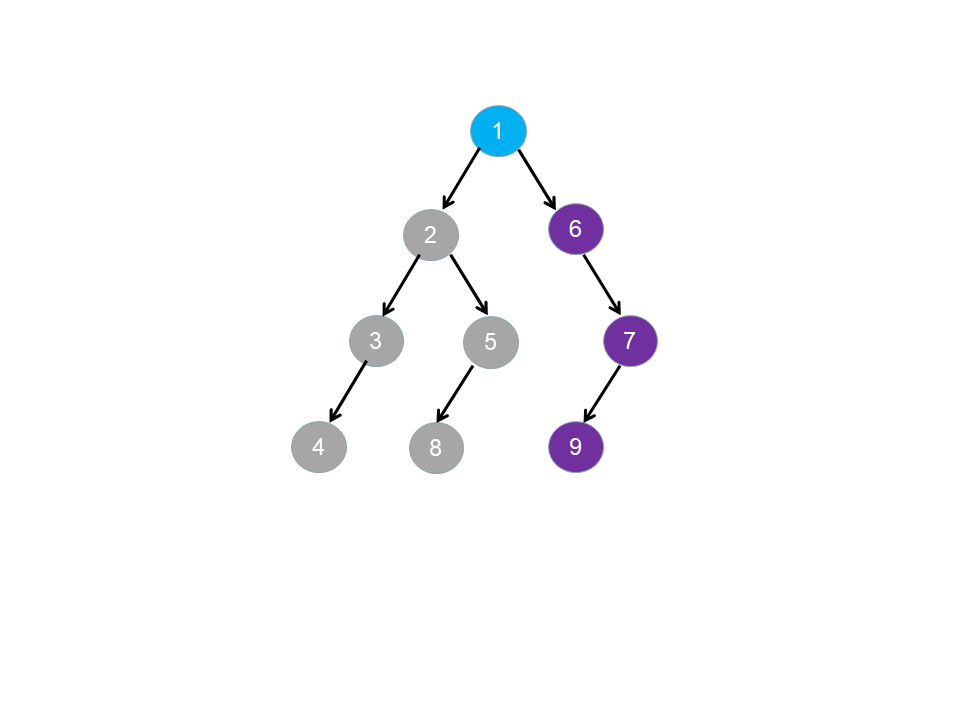
综上所述,对于 pairs 中的数对 \([x_i,y_i]\):
- 若 \(degree[x_i]>degree[y_i]\),则 \(x_i\) 为 \(y_i\) 的祖先节点;
- 若 \(degree[x_i]<degree[y_i]\),则 \(y_i\) 为 \(x_i\) 的祖先节点;
- 若 \(degree[x_i]=degree[y_i]\),则可能存在多种构造方法,\(y_i\) 为 \(x_i\) 的祖先或者 \(x_i\) 为 \(y_i\) 的祖先。
通过以上分析结论,我们可以尝试进行重新建树,并检查建成的树是否合法。
首先我们需要找到根节点 root,通过上述结论,我们找到满足 degree[root]=n−1 的节点,如果不存在根节点,则认为其不能构成合法的树,返回 0。
我们需要利用上述的结论检测是构建的树是否合法,遍历每个节点 \(node_i\),找到 \(node_i\) 的祖先 \(parent_i\),检测集合 \(adj[node_i]\) 是否为 \(adj[parent_i]\) 的子集。可以利用 \(degree[node_i]≤degree[parent_i]\) 找到所有属于 \(node_i\) 的祖先节点,然后依次检测是否满足 \(adj[node_i]∈adj[parent_i]\),如果不满足要求,则认为构建的树为非法,返回 0。
实际检测过程中不必检测节点 \(node_i\) 的所有祖先节点,只需要检测节点 \(node_i\) 的父节点是否满足子集包含的要求即可。根据上述推论找到节点 x 满足 \(degree[ x ]\) 最小且 \(degree[ x ]≥degree[node_i]\),则此时找到的节点为节点 \(node_i\) 的父亲节点,此时只需检测父亲节点是否满足上述要求即可。
设 \(node_i\) 的父节点为 parent,若满足 \(degree[node_i]=degree[parent]\) 则树的构造方式可以有多个,返回 2。
class Solution {
public:
int checkWays(vector<vector<int>>& pairs) {
unordered_map<int, unordered_set<int>> adj;
for (auto &p : pairs) {
adj[p[0]].emplace(p[1]);
adj[p[1]].emplace(p[0]);
}
/* 检测是否存在根节点*/
int root = -1;
for (auto &[node, neighbours] : adj) {
if (neighbours.size() == adj.size() - 1) {
root = node;
break;
}
}
if (root == -1) {
return 0;
}
int res = 1;
for (auto &[node, neighbours] : adj) {
if (node == root) {
continue;
}
int currDegree = neighbours.size();
int parent = -1;
int parentDegree = INT_MAX;
/* 根据 degree 的大小找到 node 的父节点 parent */
for (auto &neighbour : neighbours) {
if (adj[neighbour].size() < parentDegree && adj[neighbour].size() >= currDegree) {
parent = neighbour;
parentDegree = adj[neighbour].size();
}
}
if (parent == -1) {
return 0;
}
/* 检测 neighbours 是否是 adj[parent] 的子集 */
for (auto &neighbour : neighbours) {
if (neighbour == parent) {
continue;
}
if (!adj[parent].count(neighbour)) {
return 0;
}
}
if (parentDegree == currDegree) {
res = 2;
}
}
return res;
}
};
复杂度分析
时间复杂度:\(O(m+n^2)\),其中 n 为树中节点的数目,m 表示数组 pairs 的长度。需要遍历 pairs ,时间复杂度为 O(m),然后遍历所有的节点,检测每个节点的父节点对应的集合是否包含当前节点的对应的集合,集合中最多有 n 个元素,时间复杂度为 \(O(n^2)\),因此总的时间复杂度为 \(O(m+n^2)\)。
空间复杂度:O(m),m 表示数组 pairs 的长度。需要 O(m) 的空间来存储节点对应的集合关系。