You are given an integer n denoting the number of nodes of a weighted directed graph. The nodes are numbered from 0 to n - 1.
You are also given a 2D integer array edges where \(edges[i] = [from_i, to_i, weight_i]\) denotes that there exists a directed edge from \(from_i\) to \(to_i\) with weight \(weight_i\).
Lastly, you are given three distinct integers src1, src2, and dest denoting three distinct nodes of the graph.
Return the minimum weight of a subgraph of the graph such that it is possible to reach dest from both src1 and src2 via a set of edges of this subgraph. In case such a subgraph does not exist, return -1.
A subgraph is a graph whose vertices and edges are subsets of the original graph. The weight of a subgraph is the sum of weights of its constituent edges.
Example 1:
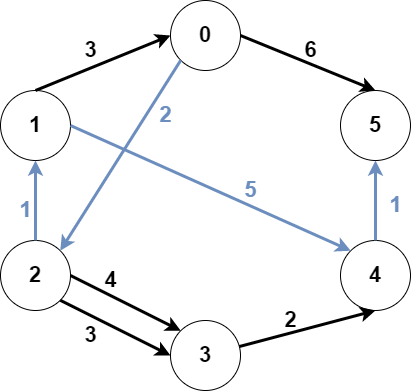
Input: n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
Output: 9
Explanation: The above figure represents the input graph. The blue edges represent one of the subgraphs that yield the optimal answer. Note that the subgraph [[1,0,3],[0,5,6]] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
Example 2:

Input: n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
Output: -1
Explanation: The above figure represents the input graph. It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
Constraints:
- \(3 <= n <= 10^5\)
- \(0 <= edges.length <= 10^5\)
edges[i].length == 30 <= fromi, toi, src1, src2, dest <= n - 1- \(from_i != to_i\)
src1,src2, anddestare pairwise distinct.- \(1 <= weight[i] <= 10^5\)
- Consider what the paths from src1 to dest and src2 to dest would look like in the optimal solution.
- It can be shown that in an optimal solution, the two paths from src1 and src2 will coincide at one node, and the remaining part to dest will be the same for both paths. Now consider how to find the node where the paths will coincide.
- How can algorithms for finding the shortest path between two nodes help us?
Solution
从 src1 和 src2 都可以到达 dest 的子图,一定是先从 src1→mid,src2→mid,然后再一起从 mid 出发,到达 dest 的形式,如下图:
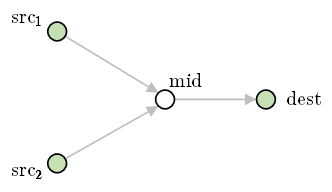
证明:若路径 src1→dest 与 src2→dest 的 第一个交点 是 mid,那么一起从 mid 走到 dest 是最优的,因为如果不一起走,那么从 mid 到 dest 就存在多条路径,此时只需选择一条最短的路径一起走,代价一定小于多条路径的权值和。
解法:
枚举中间节点 mid=i,利用 dijkstra 算法,计算
dist_src1[i]= 从 src1 出发,到达节点 i 的距离;
dist_src2[i]= 从 src2 出发,到达节点 i 的距离;
dist_dest[i]= 从 dest 出发,沿着 反向边,到达节点 i 的距离。
那么,答案就是 \(\displaystyle{\min_{0\le i \le n-1}(dist\_src1[i] + dist\_src2[i] + dist\_dest[i])}\)。
class Solution {
public:
void calc_dist(int s, vector<pair<int, int>> *graph, vector<long long int> &dist) {
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> pq;
dist[s] = 0;
pq.emplace(0, s);
while(!pq.empty()) {
auto [weight, node] = pq.top();
pq.pop();
if(weight > dist[node]) {
continue;
}
for(auto [next_node, next_weight]: graph[node]) {
if(weight + next_weight < dist[next_node]) {
dist[next_node] = weight + next_weight;
pq.emplace(weight + next_weight, next_node);
}
}
}
}
long long minimumWeight(int n, vector<vector<int>>& edges, int src1, int src2, int dest) {
vector<pair<int, int>> graph[n], graph_rev[n];
for(auto &edge: edges) {
auto from = edge[0];
auto to = edge[1];
auto weight = edge[2];
graph[from].emplace_back(to, weight);
graph_rev[to].emplace_back(from, weight);
}
long long a = LONG_LONG_MAX;
vector<long long> dist_src1(n, LONG_LONG_MAX), dist_src2(n, LONG_LONG_MAX), dist_dest(n, LONG_LONG_MAX);
calc_dist(src1, graph, dist_src1);
calc_dist(src2, graph, dist_src2);
calc_dist(dest, graph_rev, dist_dest);
long long ans = LONG_LONG_MAX;
for(int i = 0; i < n; ++i) {
if(dist_src1[i] != LONG_LONG_MAX && dist_src2[i] != LONG_LONG_MAX && dist_dest[i] != LONG_LONG_MAX) {
ans = min(ans, dist_src1[i] + dist_src2[i] + dist_dest[i]);
}
}
if(ans == LONG_LONG_MAX) {
ans = -1;
}
return ans;
}
};