azarasi / LeetCode 310. Minimum Height Trees

Created Wed, 06 Apr 2022 15:03:31 +0800 Modified Wed, 18 Sep 2024 14:00:22 +0000
2673 Words
leetcode 中等 深度优先搜索 广度优先搜索 图 拓扑排序

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h))  are called minimum height trees (MHTs).

Return a list of all MHTs’ root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

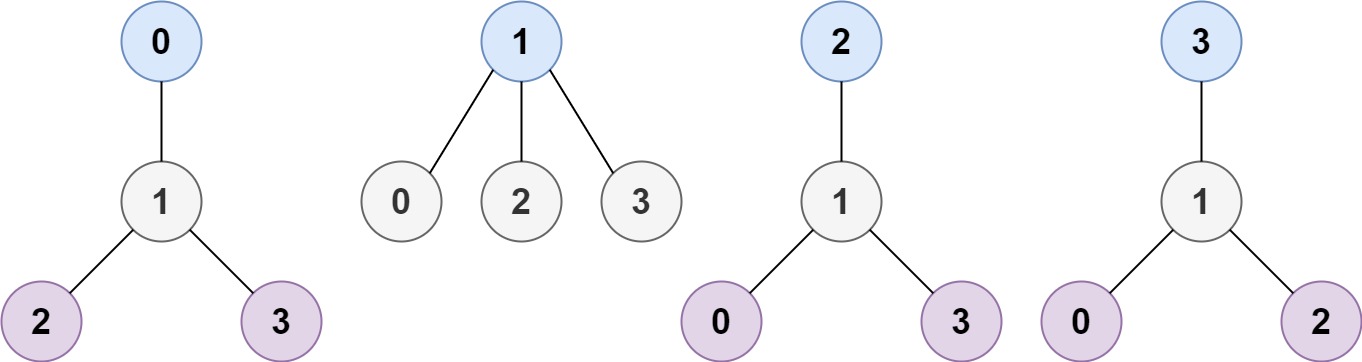
Input: n = 4, edges = [[1,0],[1,2],[1,3]]

Output: [1]

Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

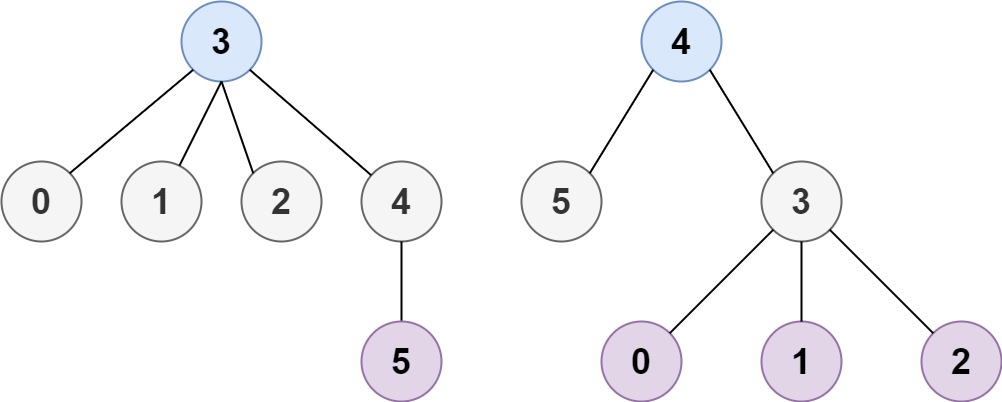
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]

Output: [3,4]

Constraints:

  • \(1 <= n <= 2 * 10^4\)
  • edges.length == n - 1
  • \(0 <= a_i, b_i < n\)
  • \(a_i != b_i\)
  • All the pairs \((a_i, b_i)\) are distinct.
  • The given input is guaranteed to be a tree and there will be no repeated edges.
  • How many MHTs can a graph have at most?

Solution

题目中给定的含有 \(n\) 个节点的树，可以推出含有以下特征

  • 任意两个节点之间有且仅有一条路径
  • 树中的共有 \(n-1\) 条不同的边
  • 叶子节点的度为 \(1\)，非叶子节点的度至少为 \(2\)
  • 树的高度由根节点到叶子节点的最大距离决定。

最直接的解法是，枚举以每个节点为根构成的树，然后求出该树的高度，所有树的最小高度即为答案，需要的时间复杂度为 \(O(n^2)\)，在此不再描述。

设 \(\textit{dist}[x][y]\) 表示从节点 \(x\) 到节点 \(y\) 的距离，假设树中距离最长的两个节点为 \((x,y)\)，它们之间的距离为 \(\textit{maxdist} = \textit{dist}[x][y]\)，则可以推出以任意节点构成的树最小高度一定为 \(\textit{minheight} = \Big \lceil \dfrac{\textit{maxdist}}{2} \Big \rceil\)，且最小高度的树根节点一定在 节点 \(x\) 到节点 \(y\) 的路径上。

  • 首先证明树的高度一定为 \(\textit{minheight} = \Big \lceil \dfrac{\textit{maxdist}}{2} \Big \rceil\)，可以用反证法证明，假设存在节点 \(z\)，以节点 \(z\) 为根的树的高度 \(h < \textit{minheight}\)，则可以推出：
    • 如果节点 \(z\) 存在于从 \(x\) 到 \(y\) 的路径上，由于 \(x\) 与 \(y\) 均为叶子节点，则可以知道 \(x\) 到 \(z\) 距离与 \(y\) 到 \(z\) 距离均小于 \(\textit{minheight}\)，\(\textit{dist}[x][y] = \textit{dist}[x][z] + \textit{dist}[z][y] \le 2 \times \Big \lceil \dfrac{\textit{dist}[x][y]}{2} \Big \rceil - 2 < \textit{dist}[x][y]\)，这与 \(x\) 到 \(y\) 的距离为 \(\textit{dist}[x][y]\) 相矛盾；
    • 如果节点 \(z\) 不存在于 \(x\) 到 \(y\) 的路径上，假设 \(z\) 到 \(x\) 的路径为 \(z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow x\)，\(z\) 到 \(y\) 的路径为 \(z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow y\)，这两个路径之间一定存在公共的交叉点，假设交叉点为 \(a\)，则可以知道此时 \(z\) 到 \(x\) 的距离为 \(\textit{dist}[z][x] = \textit{dist}[z][a] + \textit{dist}[a][z]\)，\(z\) 到 \(y\) 的距离为 \(\textit{dist}[z][y] = \textit{dist}[z][a] + \textit{dist}[a][y]\)，由于树的高度小于 \(h < \textit{minheight}\)，所以可以推出 \(\textit{dist}[z][a] + \textit{dist}[a][x] < \textit{minheight}\)，\(\textit{dist}[z][a] + \textit{dist}[a][y] < \textit{minheight}\)，即可以推出 \(\textit{dist}[a][x] + \textit{dist}[a][y] \le 2 \times \textit{minheight} - 2 = 2 \times \Big \lceil \dfrac{\textit{dist}[x][y]}{2} \Big \rceil - 2 < \textit{dist}[x][y]\)，这与 \(x\) 到 \(y\) 的距离为 \(\textit{dist}[x][y]\) 相矛盾；
  • 其次证明最小高度树的根节点一定存在于 \(x\) 到 \(y\) 的路径上，假设存在节点 \(z\) 它的最小高度为 \(\textit{minheight}\)，但节点 \(z\) 不存在于 \(x\) 到 \(y\) 之间的路径上：
    • 设 \(z\) 到 \(x\) 的路径为 \(z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow x\)，\(z\) 到 \(y\) 的路径为 \(z \rightarrow \cdots \rightarrow a \rightarrow \cdots \rightarrow y\)，这两个路径之间一定存在公共的交叉点，假设交叉点为 \(a\), 则可以知道此时 \(z\) 到 \(x\) 的距离为 \(\textit{dist}[z][x] = \textit{dist}[z][a] + \textit{dist}[a][z]\)，\(z\) 到 \(y\) 的距离为 \(\textit{dist}[z][y] = \textit{dist}[z][a] + \textit{dist}[a][y]\)，由于树的高度小 \(h = \textit{minheight}\)，所以可以推出 \(\textit{dist}[z][a] + \textit{dist}[a][x] \le \textit{minheight}\)，\(\textit{dist}[z][a] + \textit{dist}[a][y] \le \textit{minheight}\)，由于 \(z\) 不在 \(x\) 到 \(y\) 的路径上，所以可以知道 \(\textit{dist}[z][a] \ge 1\)，即可以推出 \(\textit{dist}[a][x] < \textit{minheight}，\textit{dist}[a][y] < \textit{minheight}\)，即可以推出 \(\textit{dist}[a][x] + \textit{dist}[a][y] \le 2 \times \textit{minheight} - 2 = 2 \times \Big \lceil \dfrac{\textit{dist}[x][y]}{2} \Big \rceil - 2 < \textit{dist}[x][y]\)，这与 \(x\) 到 \(y\) 的距离为 \(\textit{dist}[x][y]\) 相矛盾。

综合上述推理，设两个叶子节点的最长距离为 \(\textit{maxdist}\)，可以得到结论最小高度树的高度为 \(\Big \lceil \dfrac{\textit{maxdist}}{2} \Big \rceil\)，且最小高度树的根节点一定存在其最长路径上。

假设最长的路径的 \(m\) 个节点依次为 \(p_1 \rightarrow p_2 \rightarrow \cdots \rightarrow p_m\)，最长路径的长度为 \(m-1\)，可以得到以下结论：+ 如果 \(m\) 为偶数，此时最小高度树的根节点为 \(p_{\frac{m}{2}}\) 或者 \(p_{\frac{m}{2} + 1}\)，且此时最小的高度为 \(\dfrac{m}{2}\)；+ 如果 \(m\) 为奇数，此时最小高度树的根节点为 \(p_{\frac{m+1}{2}}\)，且此时最小的高度为 \(\dfrac{m-1}{2}\)。

因此我们只需要求出路径最长的两个叶子节点即可，并求出其路径的最中间的节点即为最小高度树的根节点。

可以利用以下算法找到图中距离最远的两个节点与它们之间的路径：+ 以任意节点 \(p\) 出现，利用广度优先搜索或者深度优先搜索找到以 \(p\) 为起点的最长路径的终点 \(x\)；+ 以节点 \(x\) 出发，找到以 \(x\) 为起点的最长路径的终点 \(y\)；+ \(x\) 到 \(y\) 之间的路径即为图中的最长路径，找到路径的中间节点即为根节点。

上述算法的证明可以参考「算法导论习题解答 9-1」。

在此我们利用广度优先搜索来找到节点的最长路径，首先找到距离节点 \(0\) 的最远节点 \(x\)，然后找到距离节点 \(x\) 的最远节点 \(y\)，然后找到节点 \(x\) 与节点 \(y\) 的路径，然后找到根节点。

复杂度分析

  • 时间复杂度：\(O(n)\)，其中 \(n\) 是为节点的个数。图中边的个数为 \(n-1\)，因此建立图的关系需要的时间复杂度为 \(O(n)\)，通过广度优先搜索需要的时间复杂度为 \(O(n + n - 1)\)，求最长路径的时间复杂度为 \(O(n)\)，因此总的时间复杂度为 \(O(n)\)。

  • 空间复杂度：\(O(n)\)，其中 \(n\) 是节点的个数。由于题目给定的图中任何两个顶点都只有一条路径连接，因此图中边的数目刚好等于 \(n-1\)，用邻接表构造图所需的空间刚好为 \(O(2 \times n)\)，存储每个节点的距离和父节点均为 \(O(n)\)，使用广度优先搜索时，队列中最多有 \(n\) 个元素，所需的空间也为 \(O(n)\)，因此空间复杂度为 \(O(n)\)。

class Solution {
public:
    int findLongestNode(int u, vector<int> & parent, vector<vector<int>>& adj) {
        int n = adj.size();
        queue<int> qu;
        vector<bool> visit(n);
        qu.emplace(u);
        visit[u] = true;
        int node = -1;

        while (!qu.empty()) {
            int curr = qu.front();
            qu.pop();
            node = curr;
            for (auto & v : adj[curr]) {
                if (!visit[v]) {
                    visit[v] = true;
                    parent[v] = curr;
                    qu.emplace(v);
                }
            }
        }
        return node;
    }

    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1) {
            return {0};
        }
        vector<vector<int>> adj(n);
        for (auto & edge : edges) {
            adj[edge[0]].emplace_back(edge[1]);
            adj[edge[1]].emplace_back(edge[0]);
        }

        vector<int> parent(n, -1);
        /* 找到与节点 0 最远的节点 x */
        int x = findLongestNode(0, parent, adj);
        /* 找到与节点 x 最远的节点 y */
        int y = findLongestNode(x, parent, adj);
        /* 求出节点 x 到节点 y 的路径 */
        vector<int> path;
        parent[x] = -1;
        while (y != -1) {
            path.emplace_back(y);
            y = parent[y];
        }
        int m = path.size();
        if (m % 2 == 0) {
            return {path[m / 2 - 1], path[m / 2]};
        } else {
            return {path[m / 2]};
        }
    }
};