给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
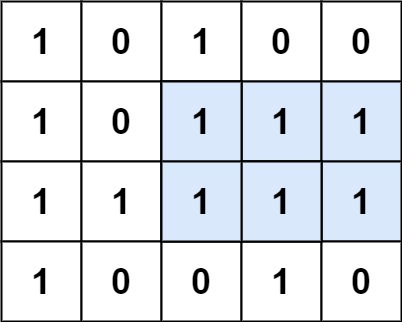
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = []
输出:0
示例 3:
输入:matrix = [["0"]]
输出:0
示例 4:
输入:matrix = [["1"]]
输出:1
示例 5:
输入:matrix = [["0","0"]]
输出:0
提示:
rows == matrix.lengthcols == matrix[0].length1 <= row, cols <= 200matrix[i][j]为'0'或'1'
题解
方法一: 使用柱状图的优化暴力方法
思路与算法
最原始地,我们可以列举每个可能的矩形。我们枚举矩形所有可能的左上角坐标和右下角坐标,并检查该矩形是否符合要求。然而该方法的时间复杂度过高,不能通过所有的测试用例,因此我们必须寻找其他方法。
我们首先计算出矩阵的每个元素的左边连续 \(1\) 的数量,使用二维数组 \(\textit{left}\) 记录,其中 \(\textit{left}[i][j]\) 为矩阵第 \(i\) 行第 \(j\) 列元素的左边连续 \(1\) 的数量。
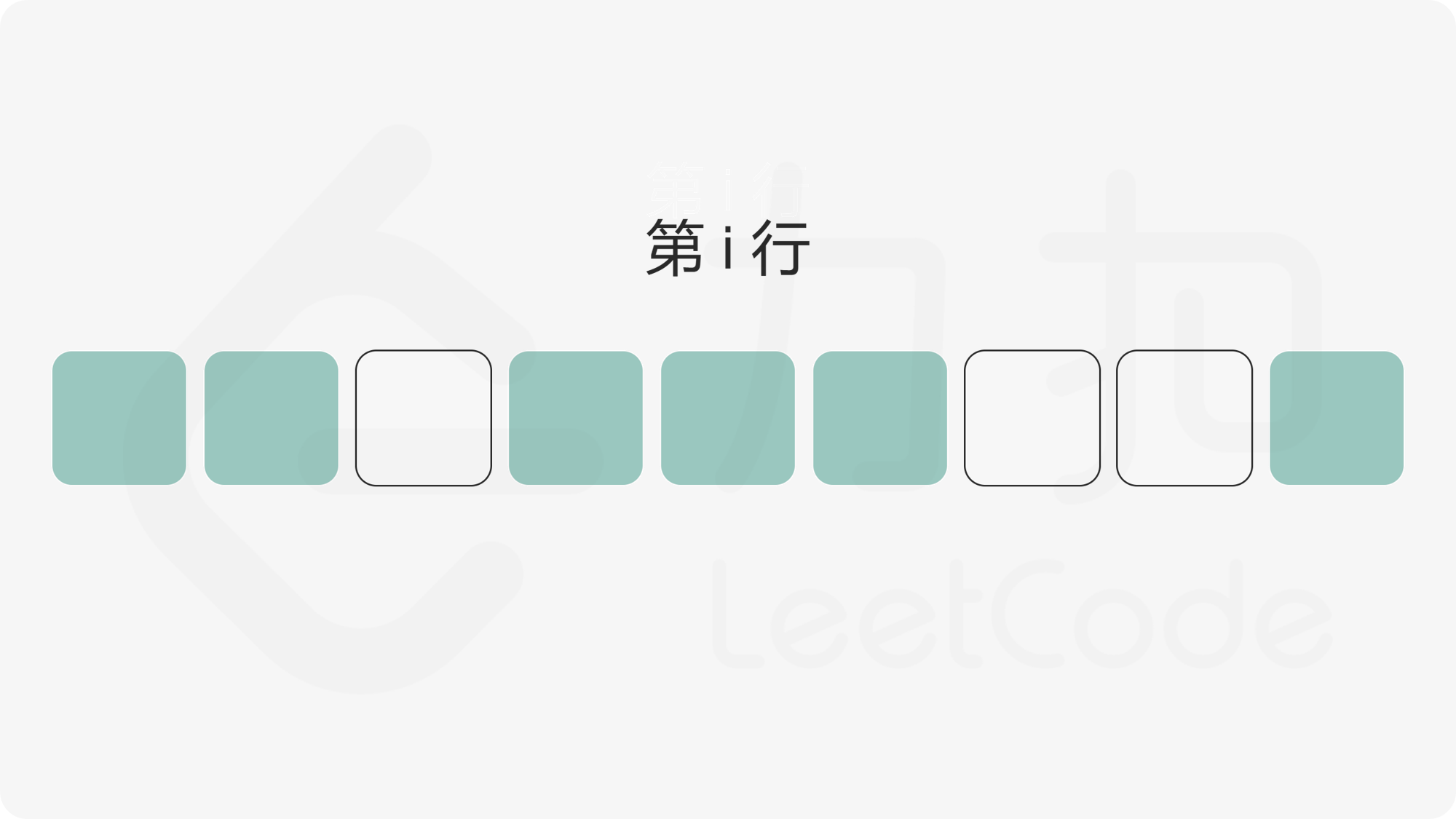
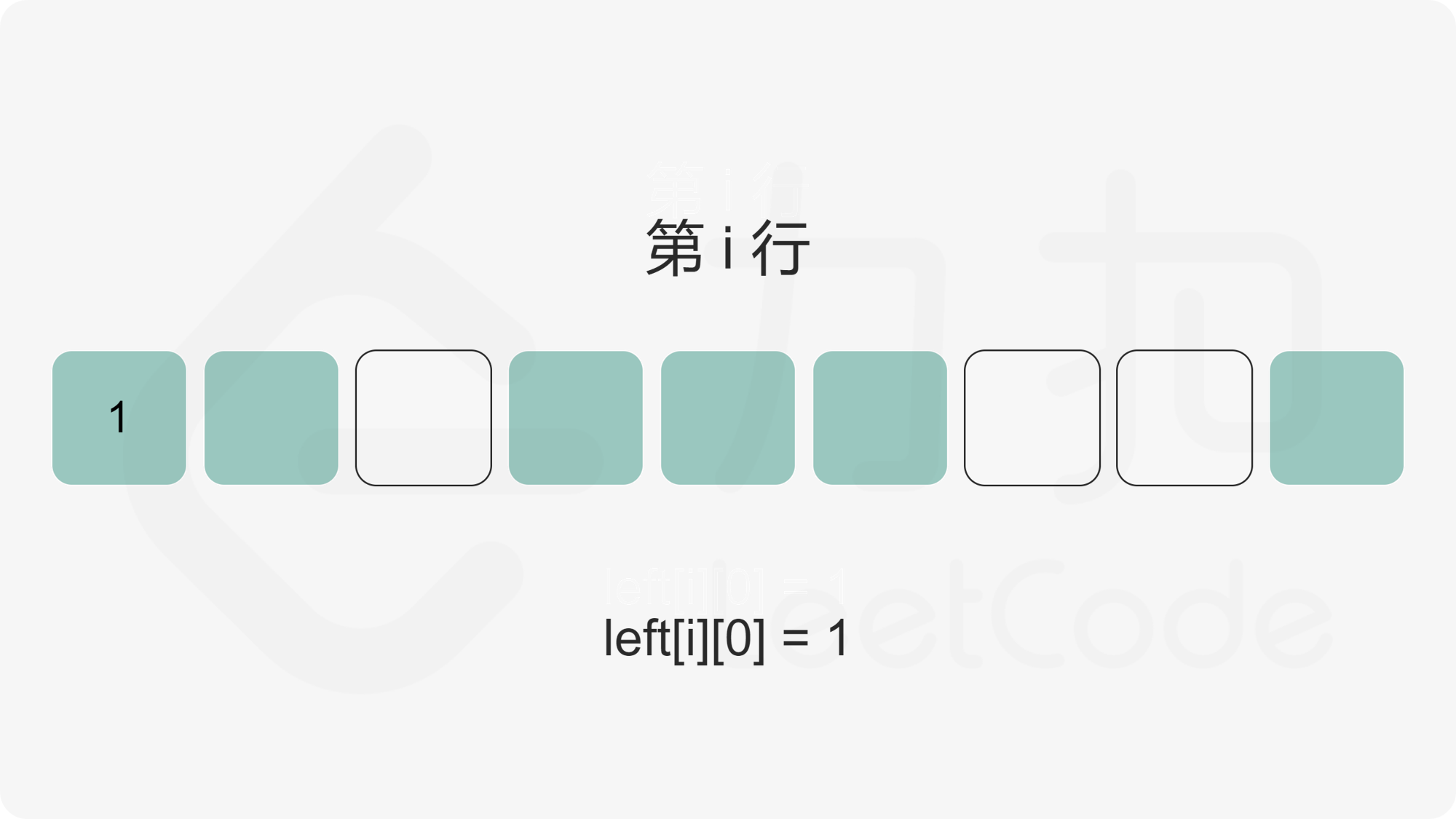
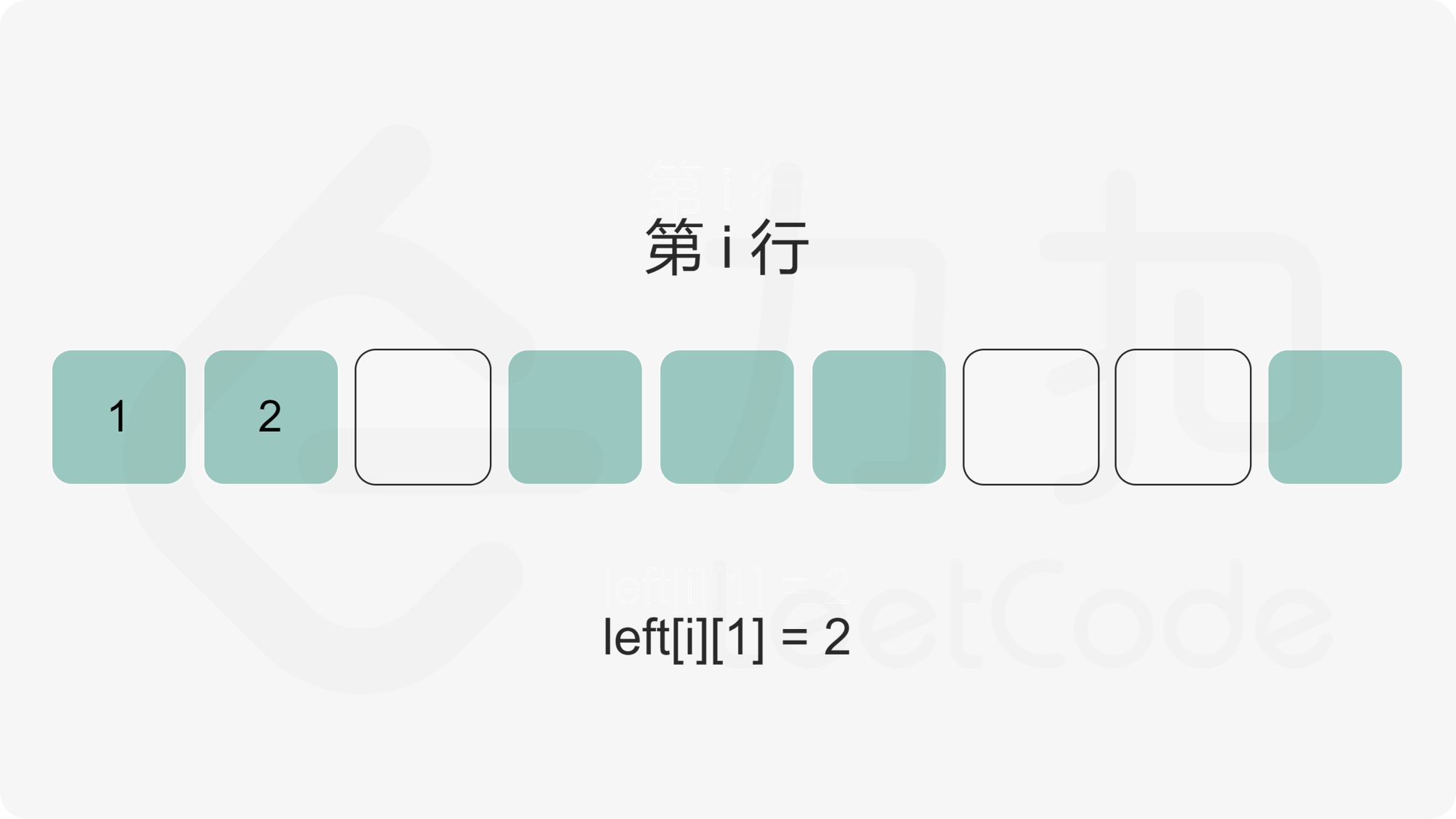
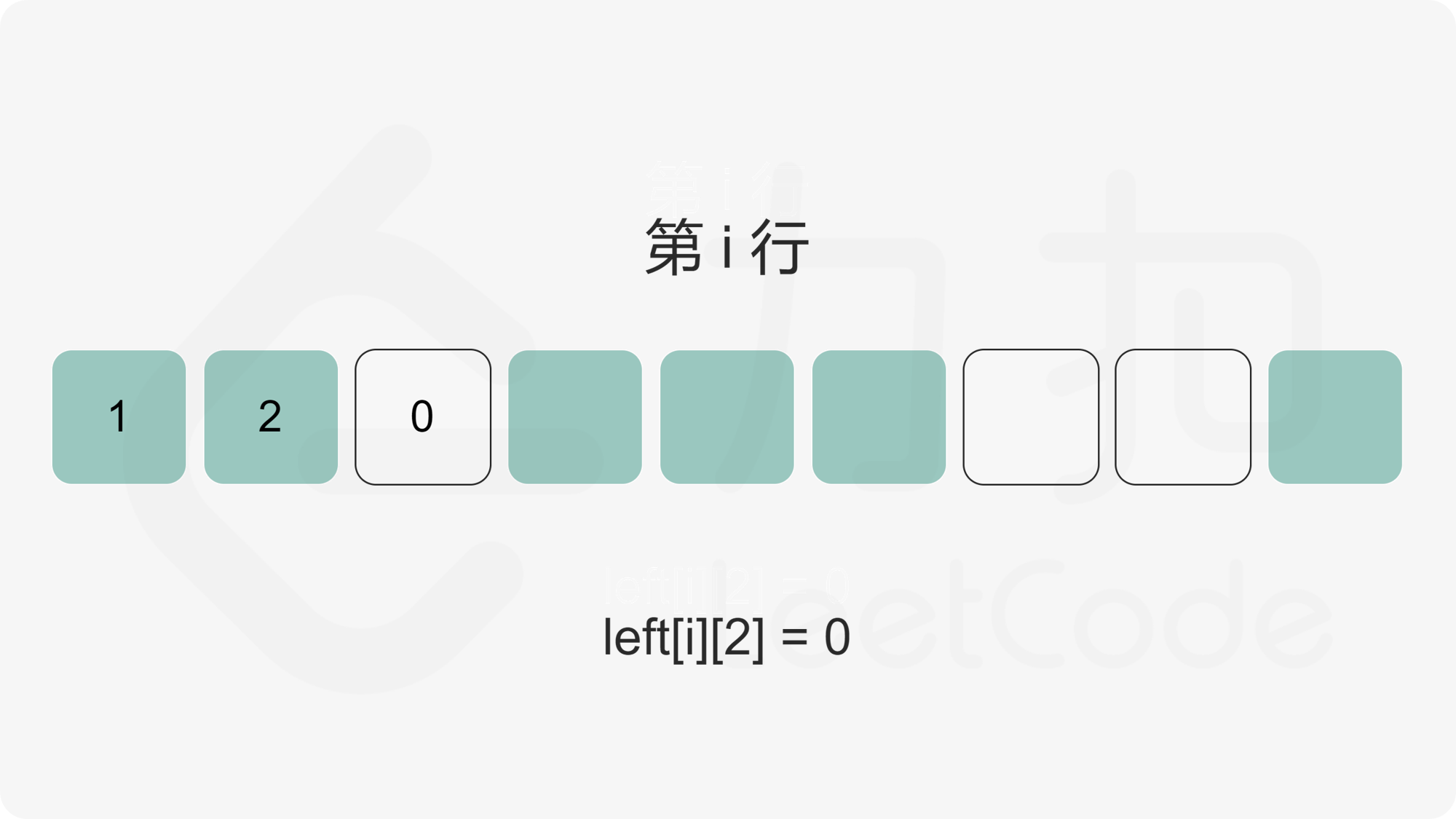
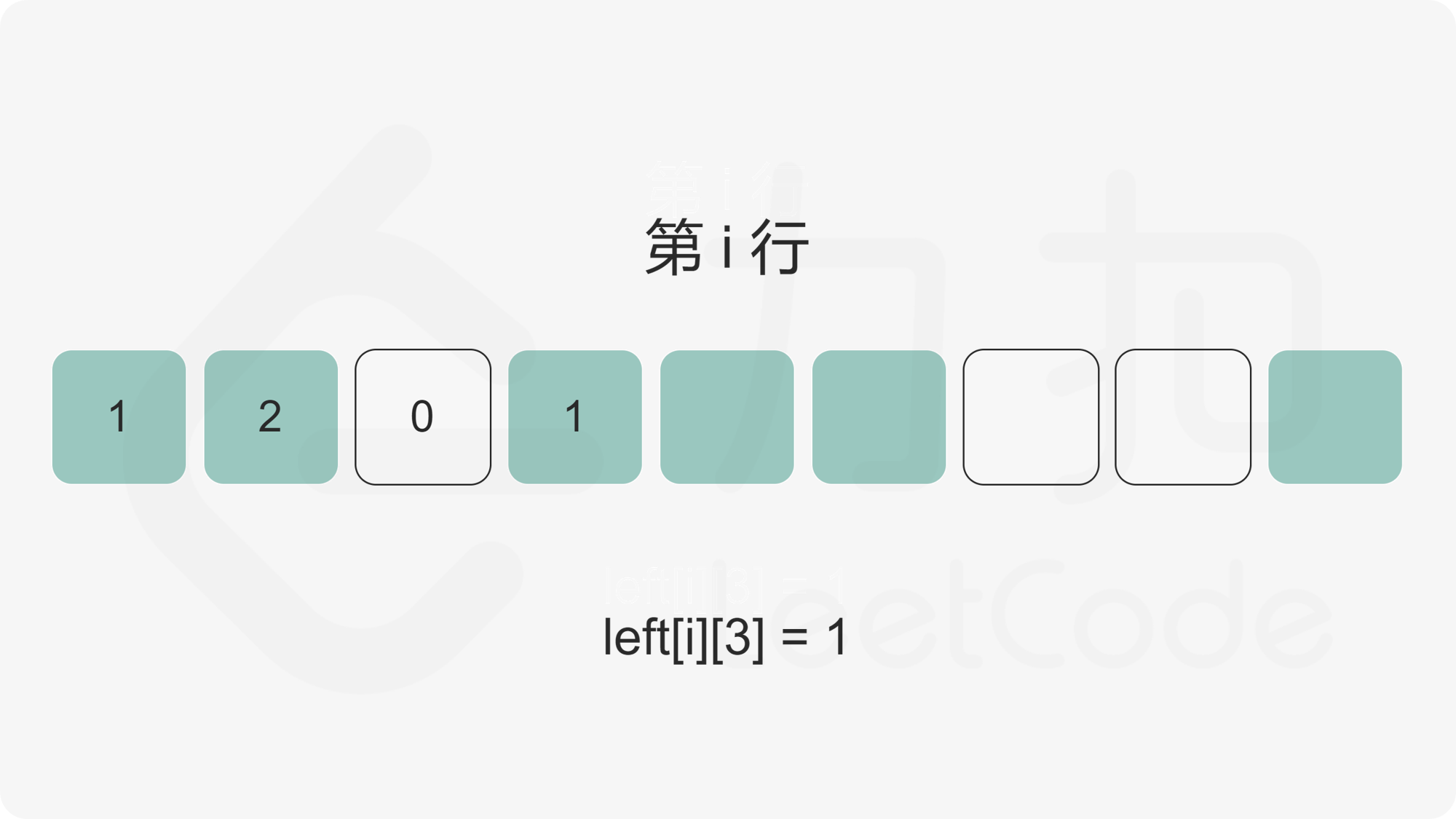
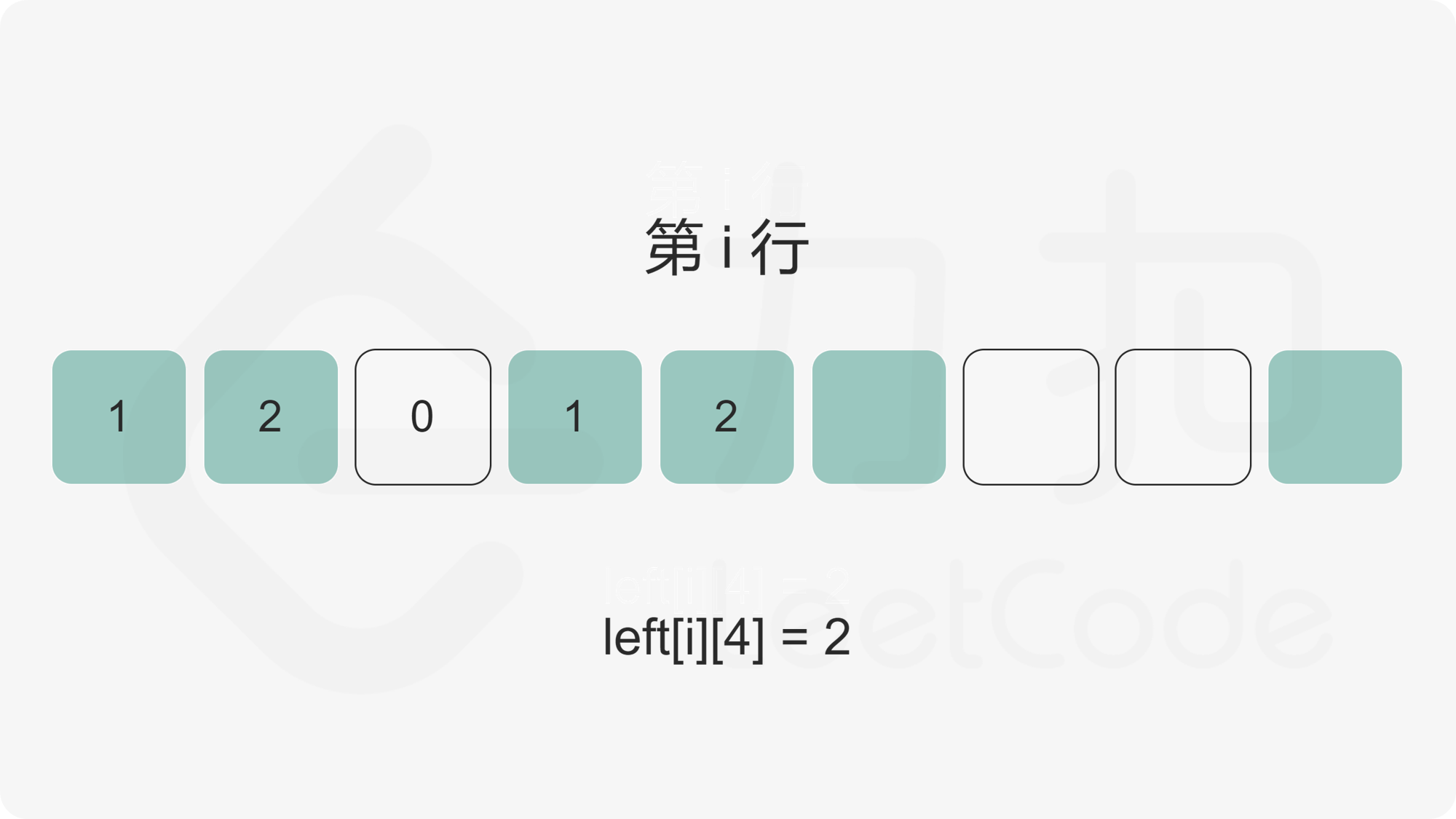
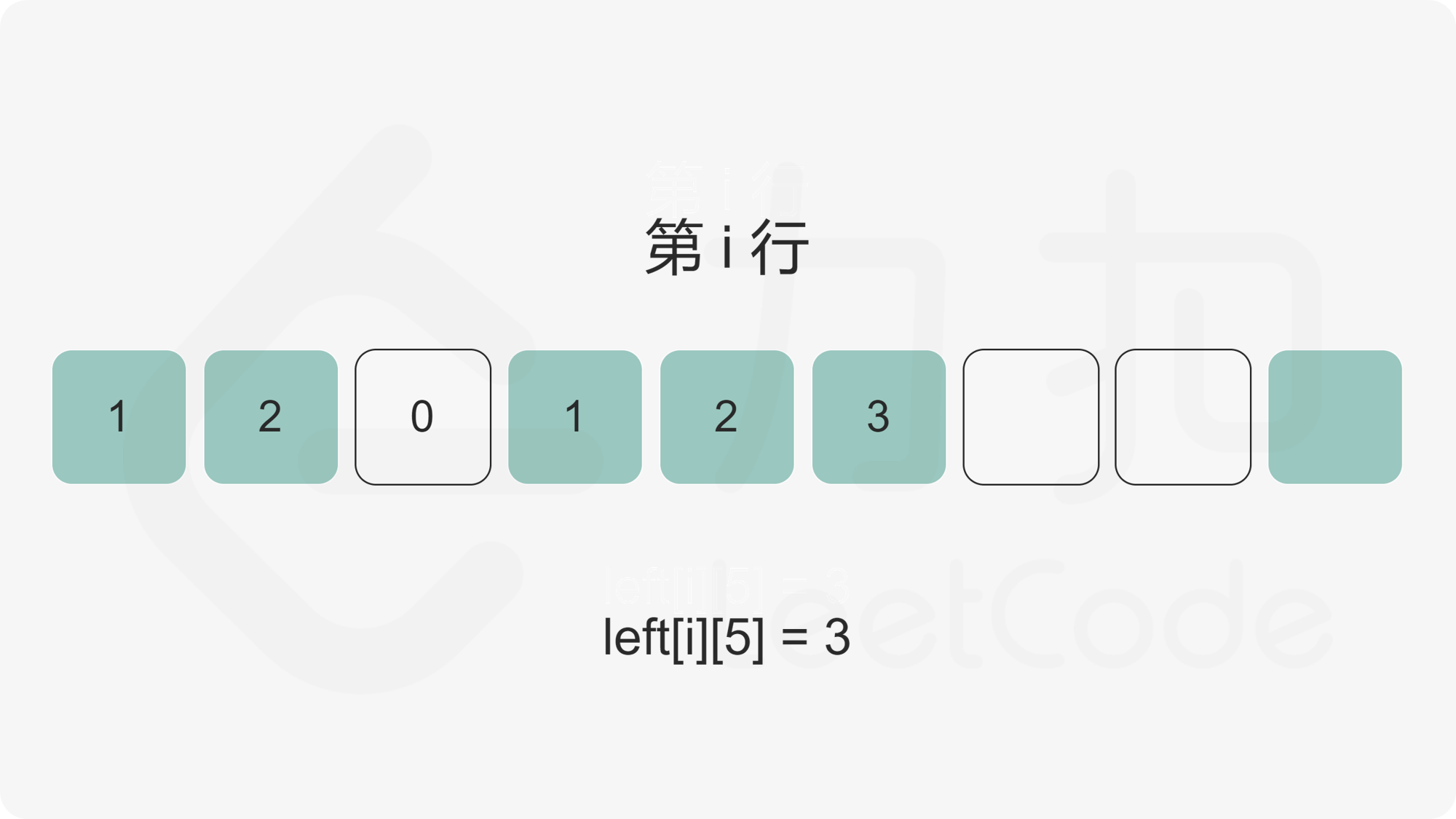
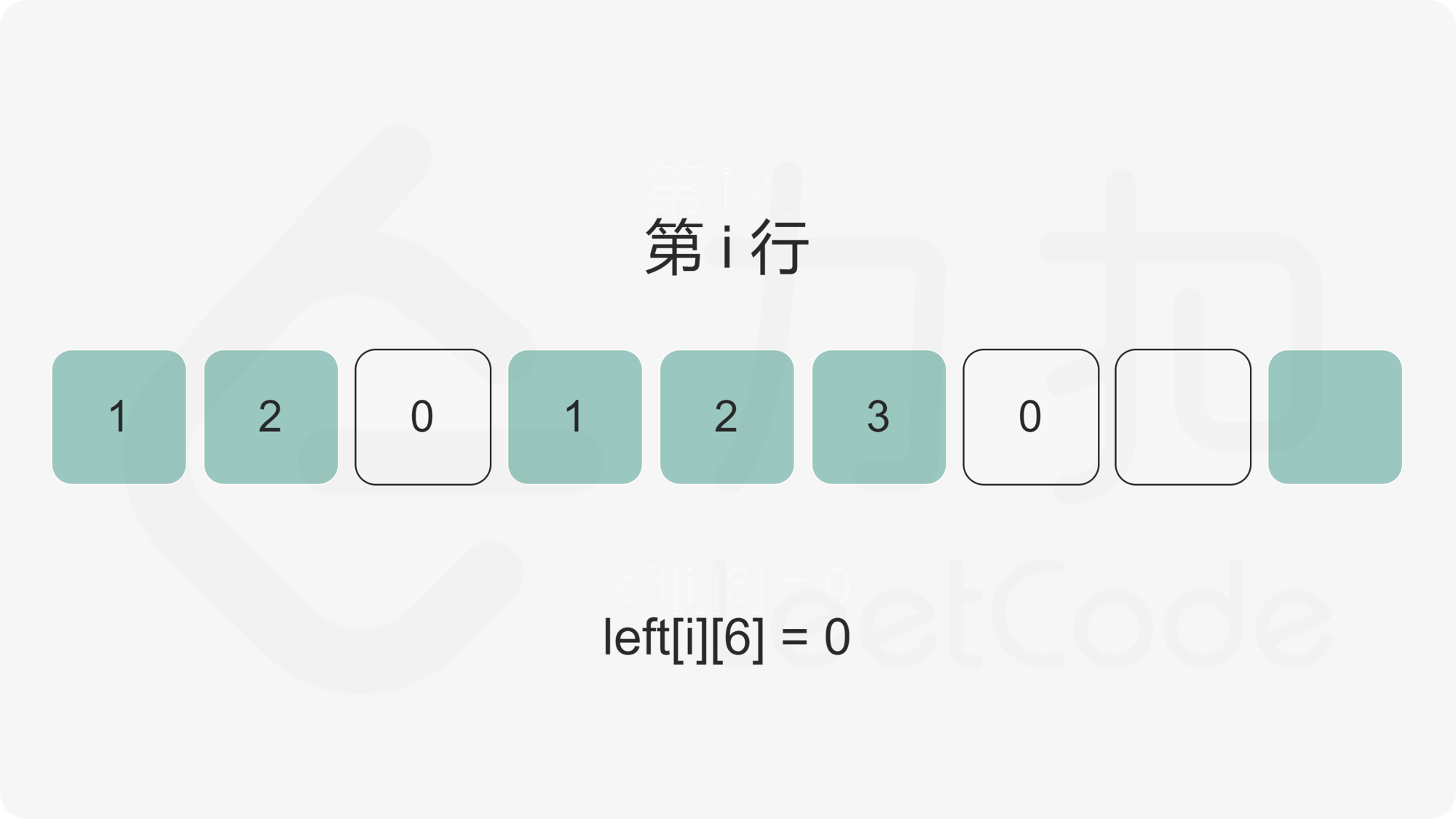
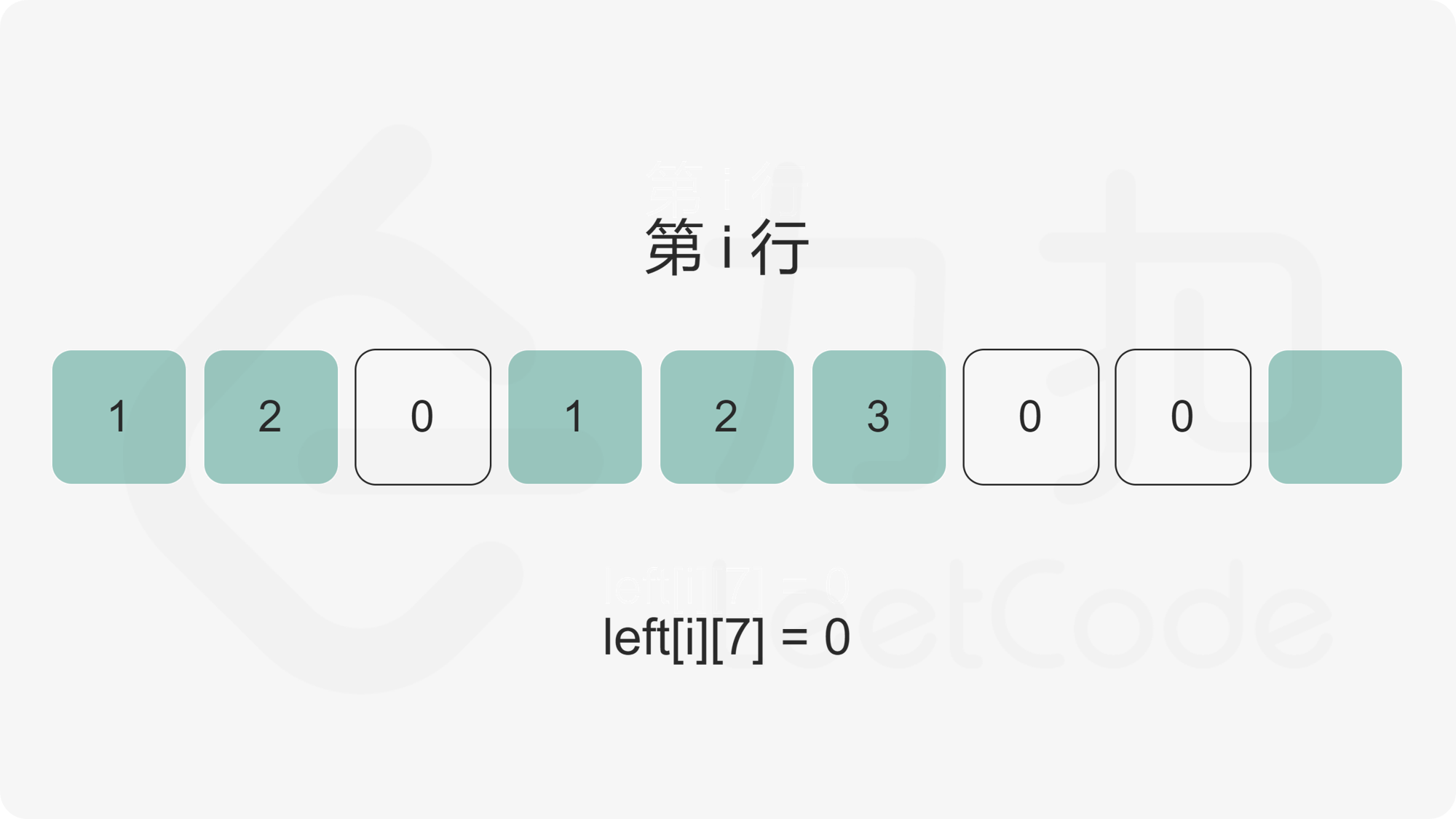
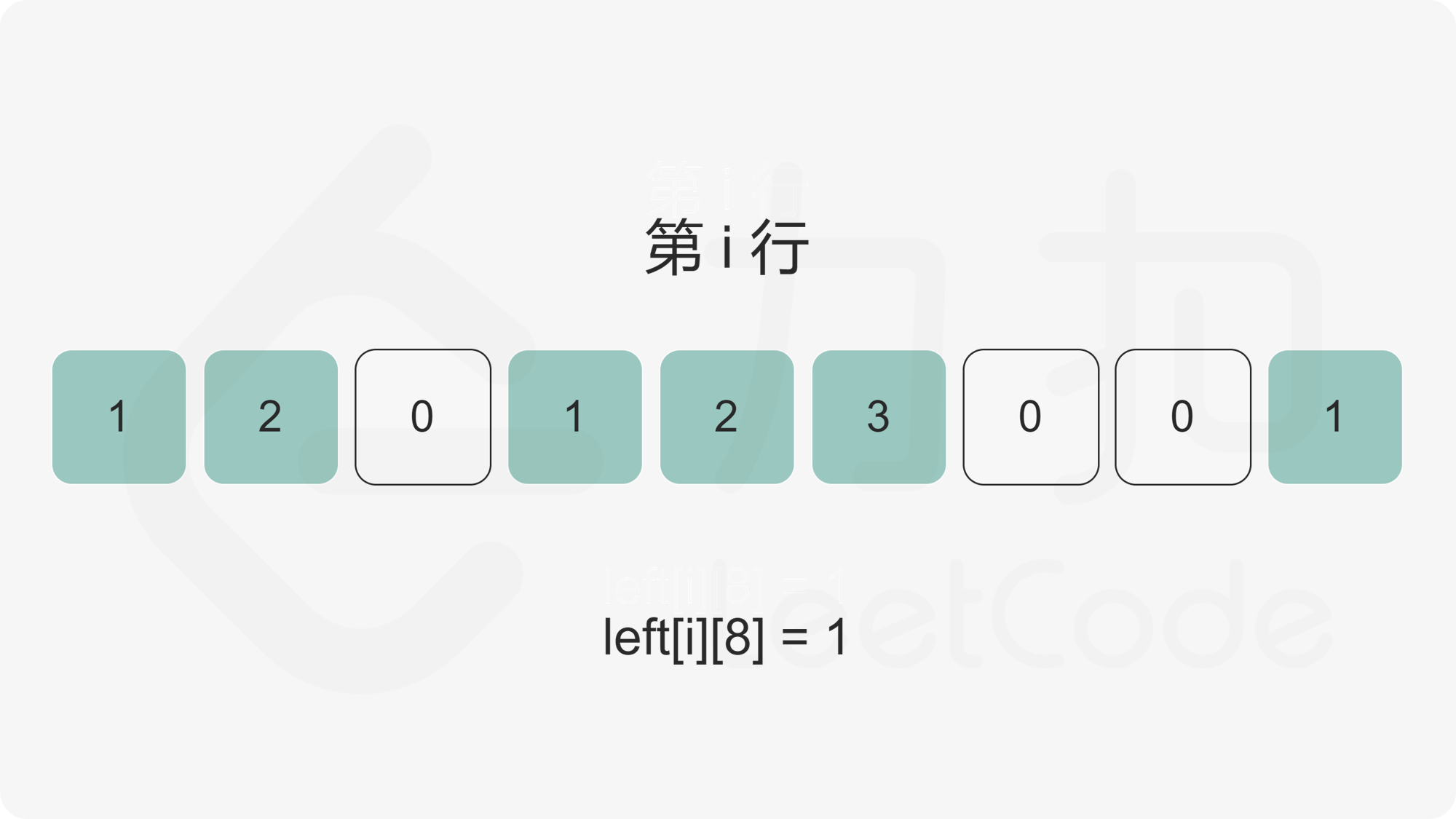
随后,对于矩阵中任意一个点,我们枚举以该点为右下角的全 \(1\) 矩形。
具体而言,当考察以 \(\textit{matrix}[i][j]\) 为右下角的矩形时,我们枚举满足 \(0 \le k \le i\) 的所有可能的 \(k\),此时矩阵的最大宽度就为
$$ \textit{left}[i][j], \textit{left}[i-1][j], \ldots, \textit{left}[k][j] $$
的最小值。
下图有助于理解。给定每个点的最大宽度,可计算出底端黄色方块的最大矩形面积。
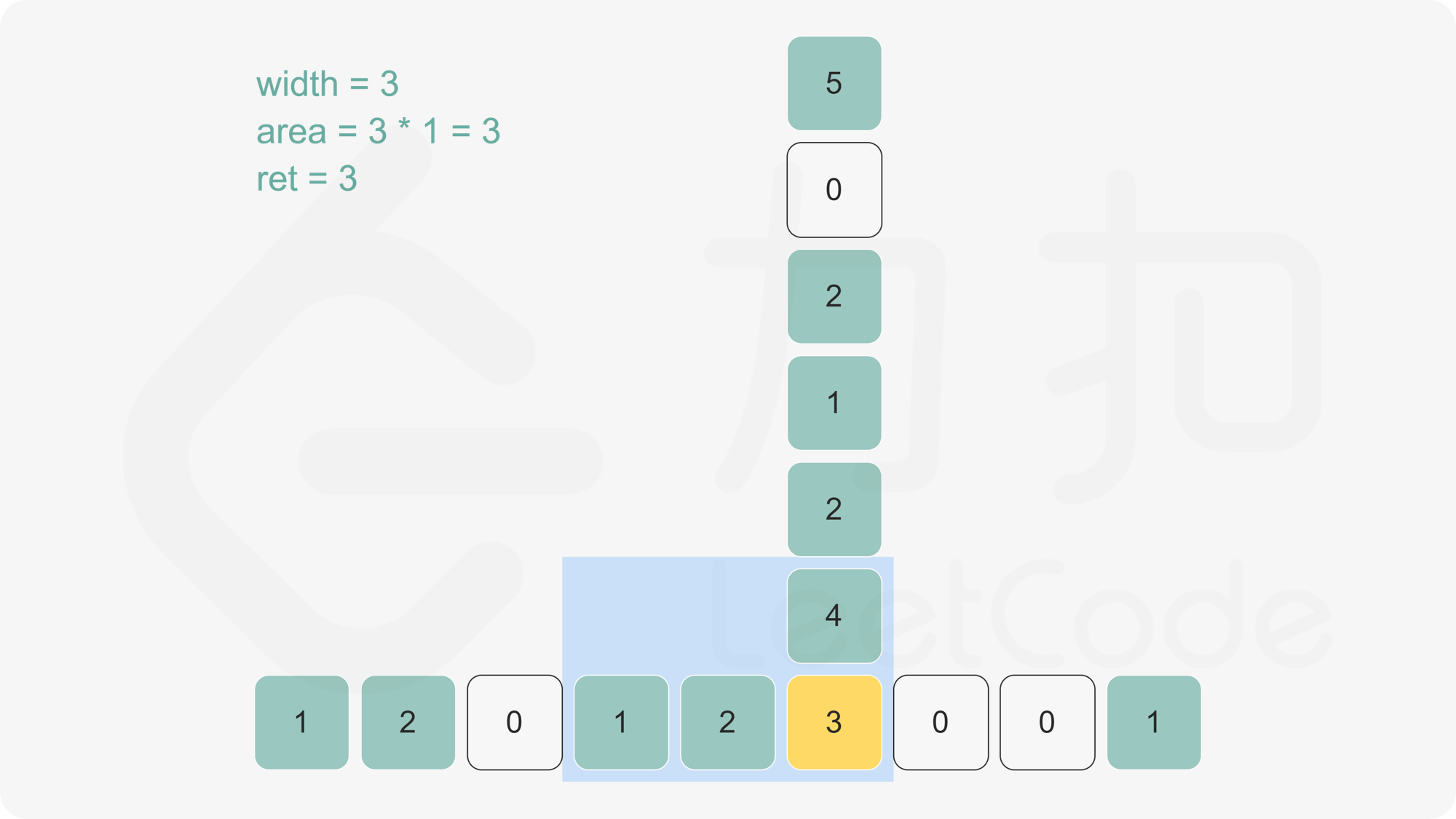
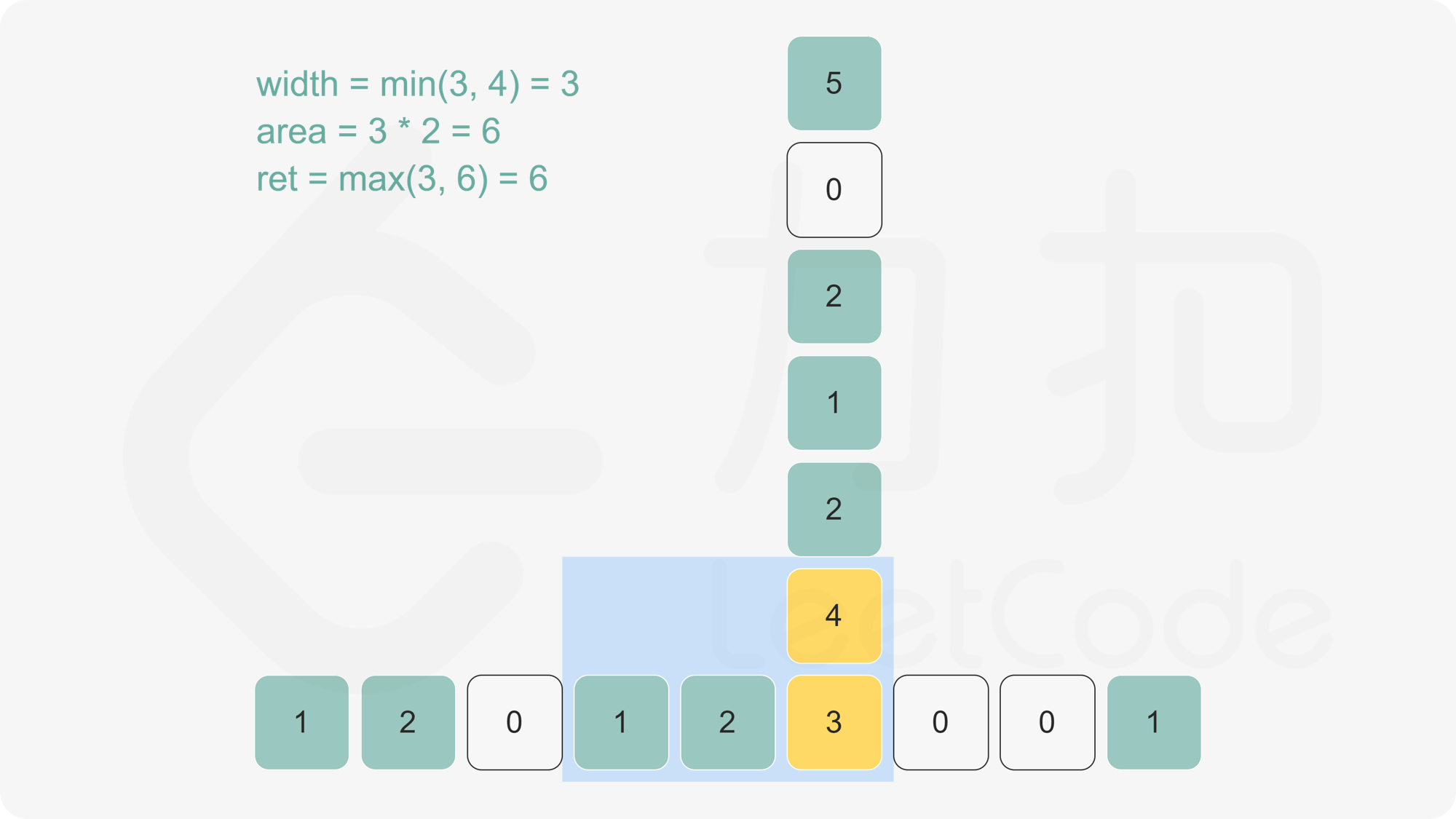
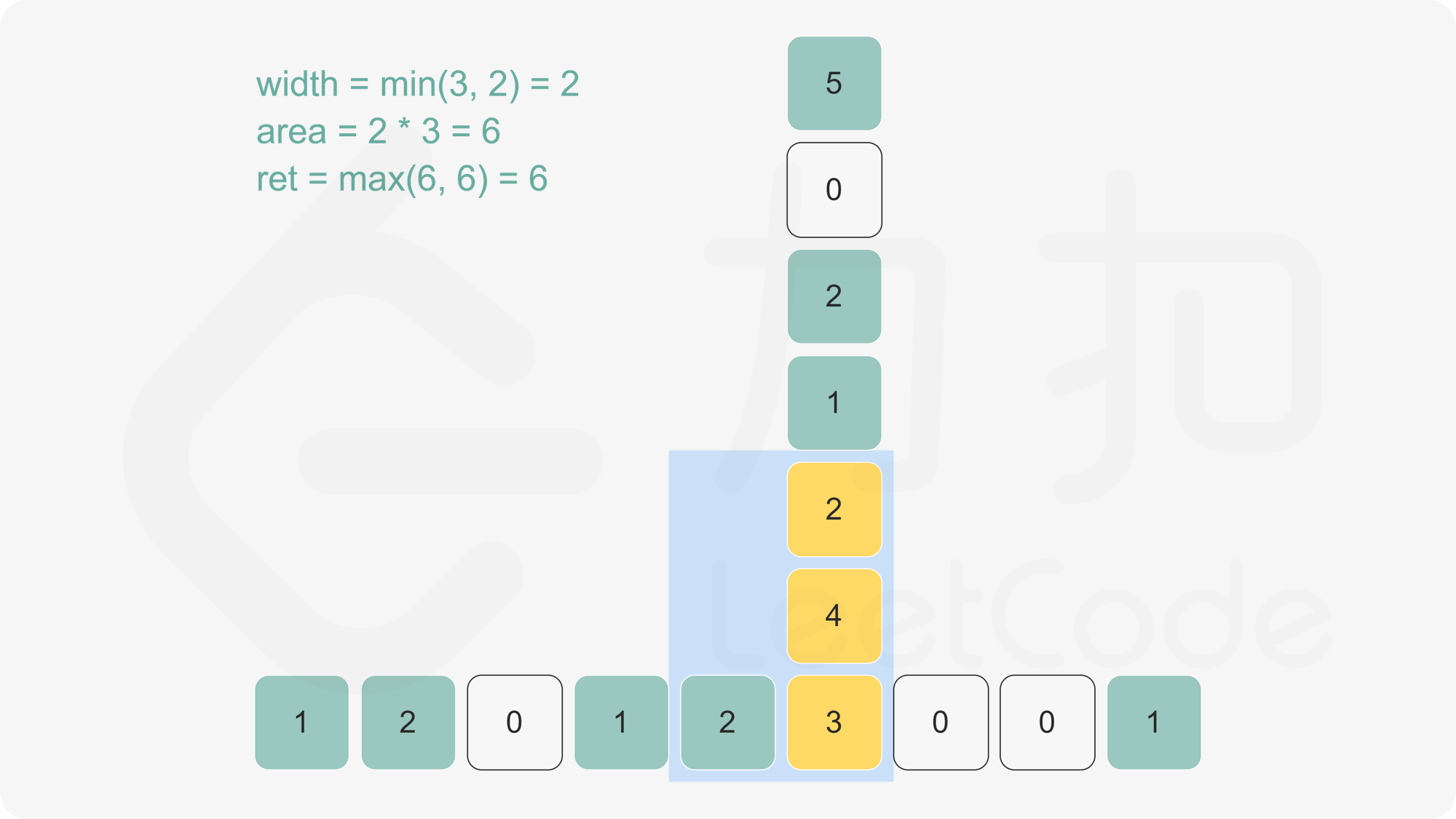
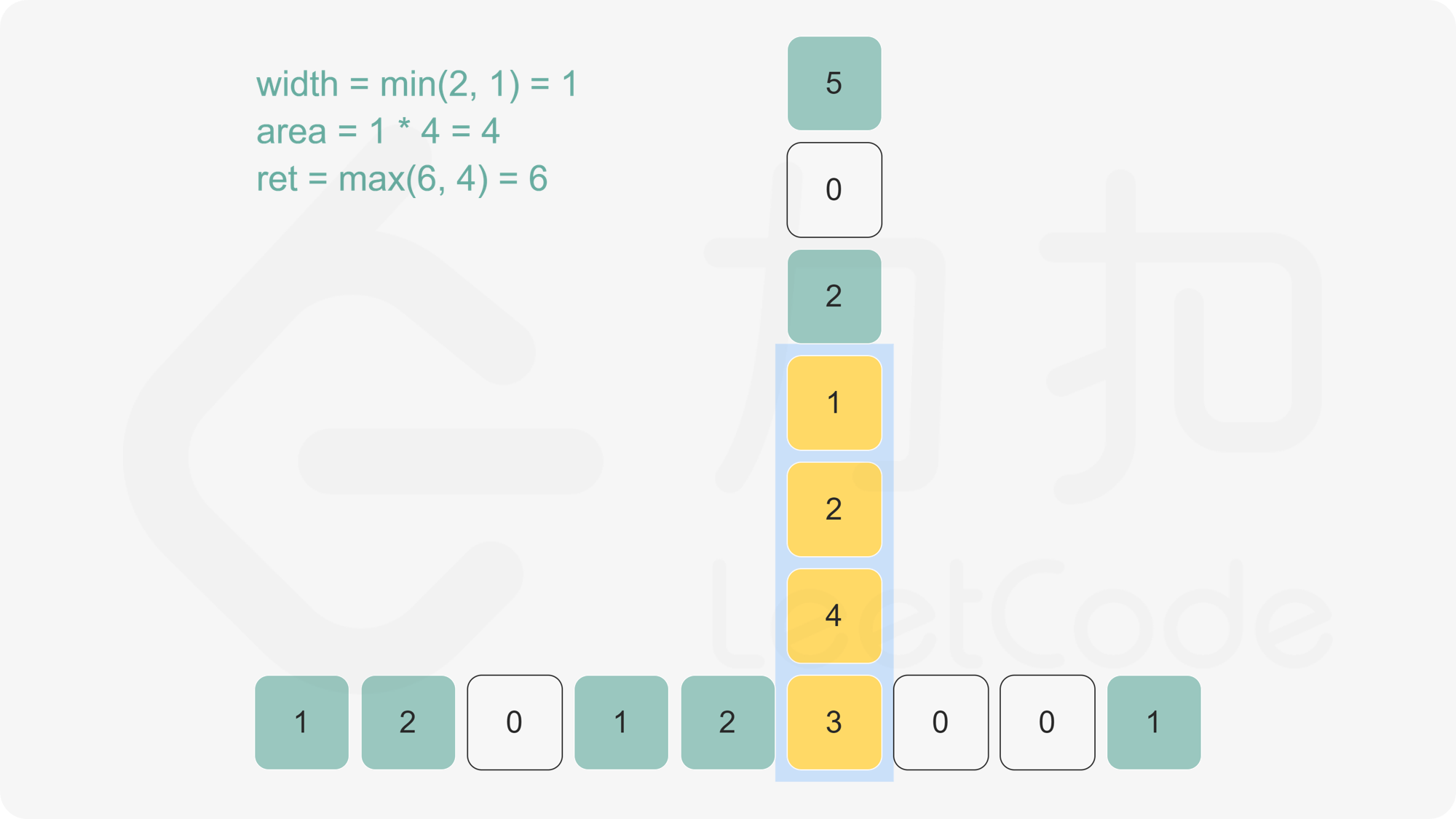
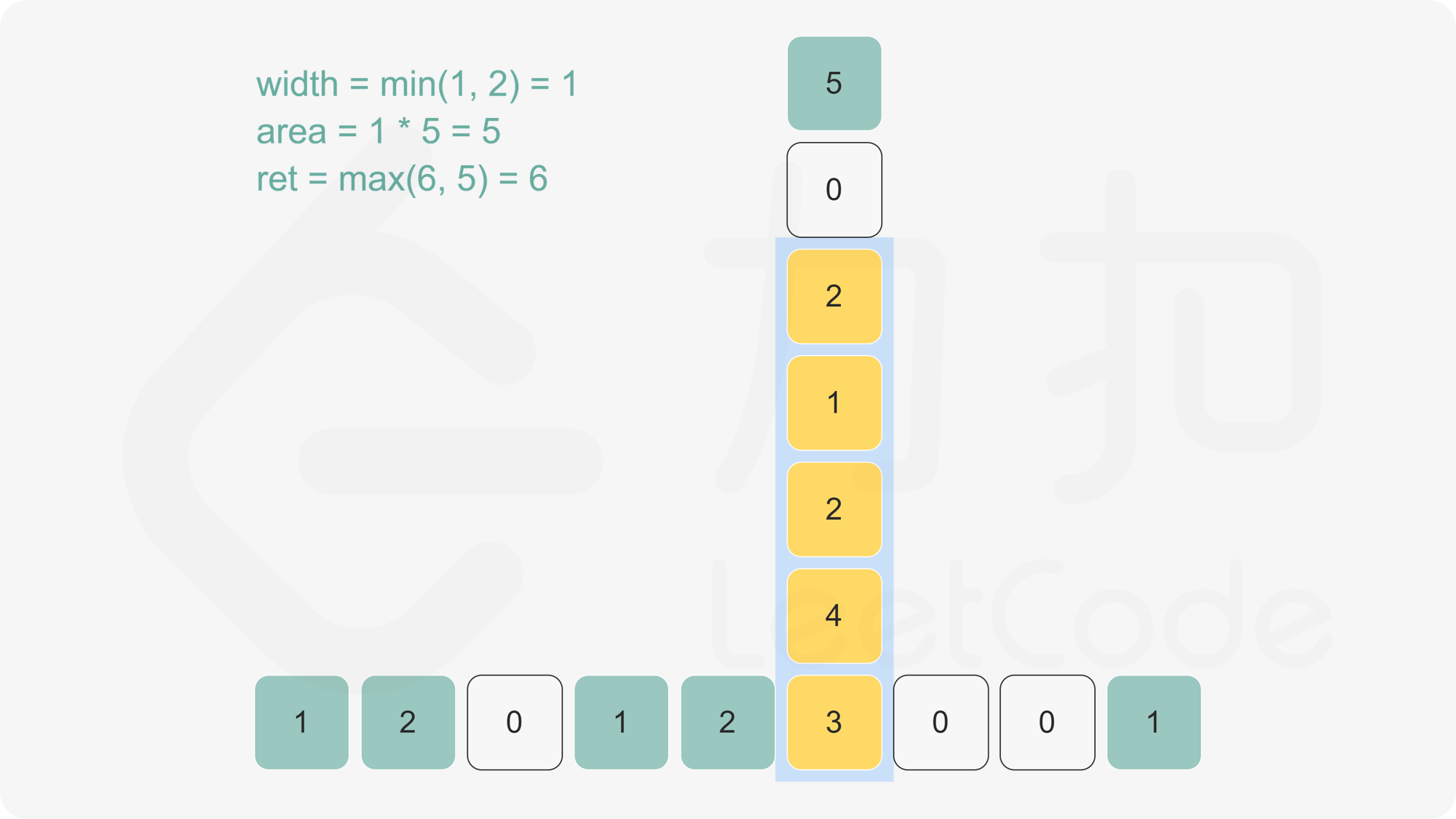
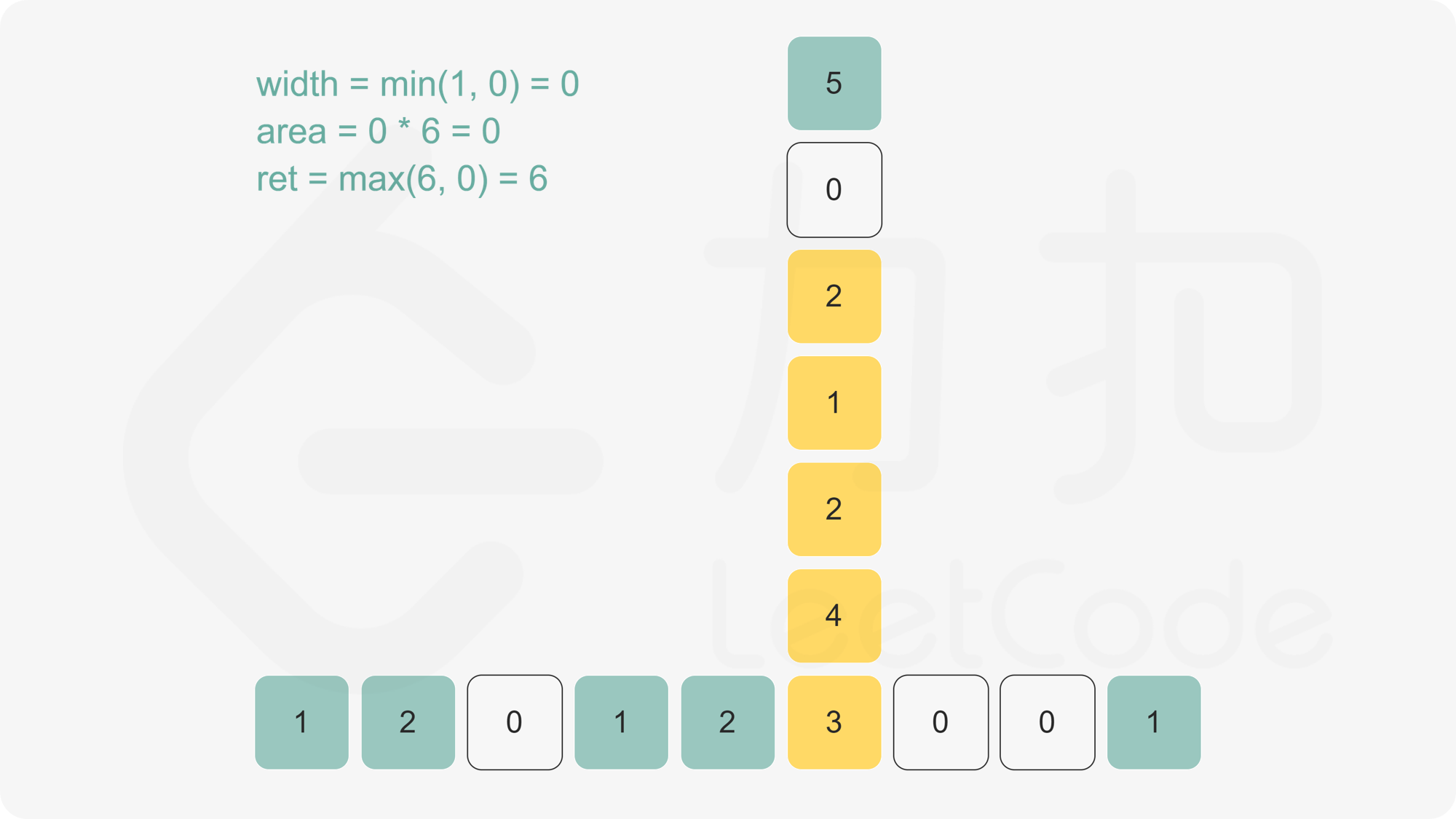
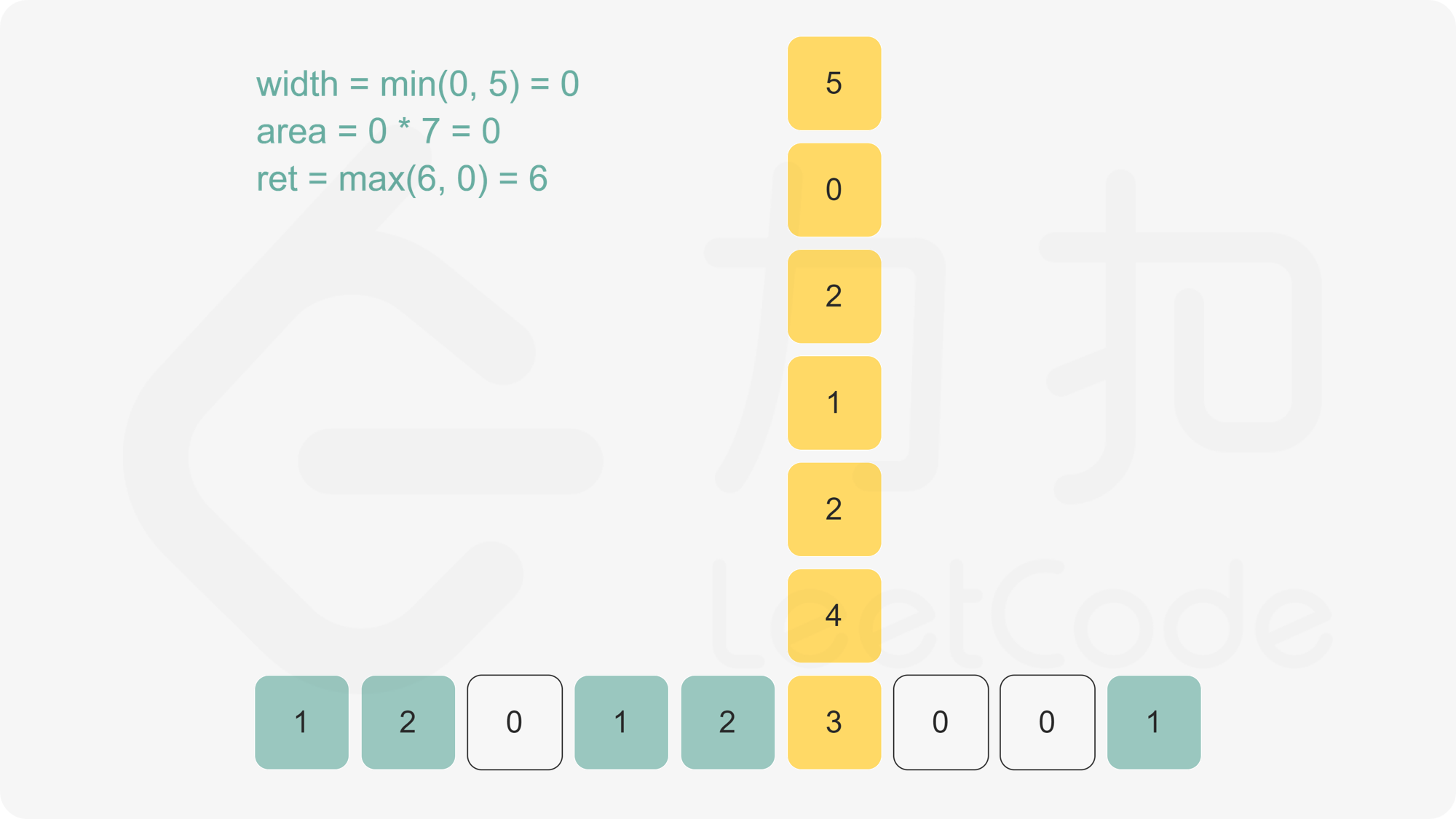 >
>
对每个点重复这一过程,就可以得到全局的最大矩形。
我们预计算最大宽度的方法事实上将输入转化成了一系列的柱状图,我们针对每个柱状图计算最大面积。
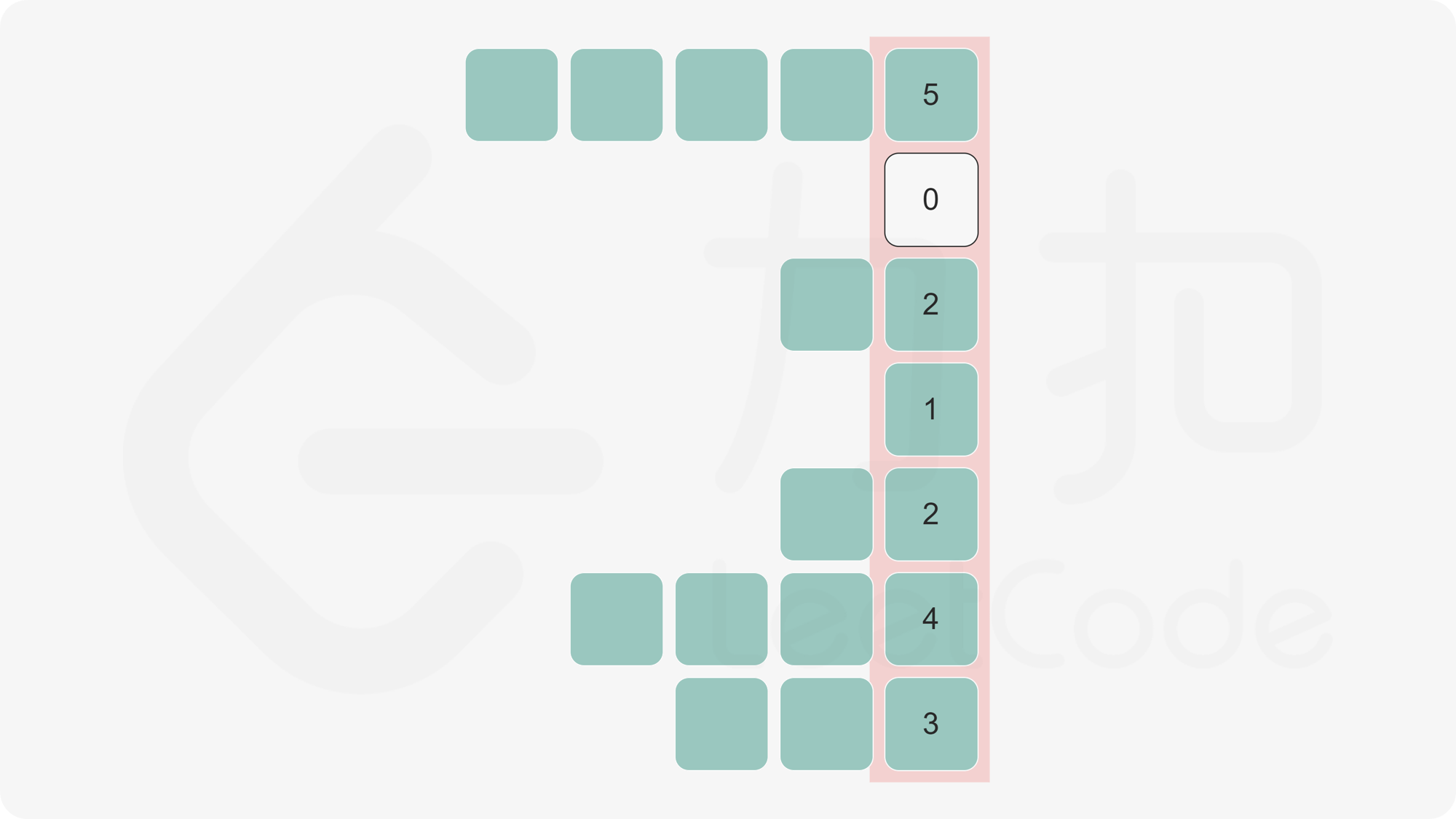
于是,上述方法本质上是「84. 柱状图中最大的矩形」题中优化暴力算法的复用。
代码
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int m = matrix.size();
if (m == 0) {
return 0;
}
int n = matrix[0].size();
vector<vector<int>> left(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
left[i][j] = (j == 0 ? 0: left[i][j - 1]) + 1;
}
}
}
int ret = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '0') {
continue;
}
int width = left[i][j];
int area = width;
for (int k = i - 1; k >= 0; k--) {
width = min(width, left[k][j]);
area = max(area, (i - k + 1) * width);
}
ret = max(ret, area);
}
}
return ret;
}
};
复杂度分析
时间复杂度:\(O(m^2n)\),其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。计算 \(\textit{left}\) 矩阵需要 \(O(mn)\) 的时间。随后对于矩阵的每个点,需要 \(O(m)\) 的时间枚举高度。故总的时间复杂度为 \(O(mn) + O(mn) \cdot O(m) = O(m^2n)\)。
空间复杂度:\(O(mn)\),其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。我们分配了一个与给定矩阵等大的数组,用于存储每个元素的左边连续 \(1\) 的数量。
方法二:单调栈
思路与算法
在方法一中,我们讨论了将输入拆分成一系列的柱状图。为了计算矩形的最大面积,我们只需要计算每个柱状图中的最大面积,并找到全局最大值。
我们可以使用「84. 柱状图中最大的矩形的官方题解」中的单调栈的做法,将其应用在我们生成的柱状图中。
代码
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int m = matrix.size();
if (m == 0) {
return 0;
}
int n = matrix[0].size();
vector<vector<int>> left(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
left[i][j] = (j == 0 ? 0: left[i][j - 1]) + 1;
}
}
}
int ret = 0;
for (int j = 0; j < n; j++) { // 对于每一列,使用基于柱状图的方法
vector<int> up(m, 0), down(m, 0);
stack<int> stk;
for (int i = 0; i < m; i++) {
while (!stk.empty() && left[stk.top()][j] >= left[i][j]) {
stk.pop();
}
up[i] = stk.empty() ? -1 : stk.top();
stk.push(i);
}
stk = stack<int>();
for (int i = m - 1; i >= 0; i--) {
while (!stk.empty() && left[stk.top()][j] >= left[i][j]) {
stk.pop();
}
down[i] = stk.empty() ? m : stk.top();
stk.push(i);
}
for (int i = 0; i < m; i++) {
int height = down[i] - up[i] - 1;
int area = height * left[i][j];
ret = max(ret, area);
}
}
return ret;
}
};
读者可以自行比对上面的代码与此前第 84 题的代码的相似之处。
复杂度分析
时间复杂度:\(O(mn)\),其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。计算 \(\textit{left}\) 矩阵需要 \(O(mn)\) 的时间;对每一列应用柱状图算法需要 \(O(m)\) 的时间,一共需要 \(O(mn)\) 的时间。
空间复杂度:\(O(mn)\),其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。我们分配了一个与给定矩阵等大的数组,用于存储每个元素的左边连续 \(1\) 的数量。