Given a string s, return the longest palindromic substring in s.
Example 1:
Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.
Example 2:
Input: s = "cbbd"
Output: "bb"
Constraints:
1 <= s.length <= 1000sconsist of only digits and English letters.
题解
方法一:动态规划
思路与算法
对于一个子串而言,如果它是回文串,并且长度大于 \(2\),那么将它首尾的两个字母去除之后,它仍然是个回文串
例如对于字符串 \(\textrm{‘‘ababa’’}\),如果我们已经知道 \(\textrm{‘‘bab’’}\) 是回文串,那么 \(\textrm{‘‘ababa’’}\) 一定是回文串,这是因为它的首尾两个字母都是 \(\textrm{‘‘a’’}\)。
根据这样的思路,我们就可以用动态规划的方法解决本题。我们用 \(P(i,j)\) 表示字符串 \(s\) 的第 \(i\) 到 \(j\) 个字母组成的串(下文表示成 \(s[i:j]\))是否为回文串:
$$ P(i,j) = \begin{cases} \text{true,} &\quad\text{如果子串~} S_i \dots S_j \text{~是回文串} \ \text{false,} &\quad\text{其它情况} \end{cases} $$
这里的「其它情况」包含两种可能性
\(s[i, j]\) 本身不是一个回文串
\(i > j\),此时 \(s[i, j]\) 本身不合法。
那么我们就可以写出动态规划的状态转移方程:
$$ P(i, j) = P(i+1, j-1) \wedge (S_i == S_j) $$
也就是说,只有 \(s[i+1:j-1]\) 是回文串,并且 \(s\) 的第 \(i\) 和 \(j\) 个字母相同时,\(s[i:j]\) 才会是回文串。
上文的所有讨论是建立在子串长度大于 \(2\) 的前提之上的,我们还需要考虑动态规划中的边界条件,即子串的长度为 \(1\) 或 \(2\)。
对于长度为 \(1\) 的子串,它显然是个回文串;对于长度为 \(2\) 的子串,只要它的两个字母相同,它就是一个回文串。
因此我们就可以写出动态规划的边界条件:
$$ \begin{cases}P(i, i) = \text{true} \ P(i, i+1) = ( S_i == S_{i+1} )\end{cases} $$
根据这个思路,我们就可以完成动态规划了,最终的答案即为所有 \(P(i, j) = \text{true}\) 中 \(j-i+1\)(即子串长度)的最大值。
注意:在状态转移方程中,我们是从长度较短的字符串向长度较长的字符串进行转移的,因此一定要注意动态规划的循环顺序。
#include <iostream>
#include <string>
#include <vector>
using namespace std;
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if (n < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
vector<vector<int>> dp(n, vector<int>(n));
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= n; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < n; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= n) {
break;
}
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, maxLen);
}
};
复杂度分析
- 时间复杂度:\(O(n^2)\),其中 \(n\) 是字符串的长度。
动态规划的状态总数为 \(O(n^2)\),对于每个状态,我们需要转移的时间为 \(O(1)\)。
- 空间复杂度:\(O(n^2)\),即存储动态规划状态需要的空间。
方法二:中心扩展算法
思路与算法
我们仔细观察一下方法一中的状态转移方程:
$$ \begin{cases} P(i, i) &=\quad \text{true} \ P(i, i+1) &=\quad ( S_i == S_{i+1} ) \ P(i, j) &=\quad P(i+1, j-1) \wedge (S_i == S_j)\end{cases} $$
找出其中的状态转移链:
$$ P(i, j) \leftarrow P(i+1, j-1) \leftarrow P(i+2, j-2) \leftarrow \cdots \leftarrow \text{某一边界情况} $$
可以发现,所有的状态在转移的时候的可能性都是唯一的
也就是说,我们可以从每一种边界情况开始「扩展」,也可以得出所有的状态对应的答案。
边界情况即为子串长度为 \(1\) 或 \(2\) 的情况。
我们枚举每一种边界情况,并从对应的子串开始不断地向两边扩展。
如果两边的字母相同,我们就可以继续扩展,例如从 \(P(i+1,j-1)\) 扩展到 \(P(i,j)\);如果两边的字母不同,我们就可以停止扩展,因为在这之后的子串都不能是回文串了。
聪明的读者此时应该可以发现,「边界情况」对应的子串实际上就是我们「扩展」出的回文串的「回文中心」。
方法二的本质即为:我们枚举所有的「回文中心」并尝试「扩展」,直到无法扩展为止,此时的回文串长度即为此「回文中心」下的最长回文串长度。
我们对所有的长度求出最大值,即可得到最终的答案。
class Solution {
public:
pair<int, int> expandAroundCenter(const string& s, int left, int right) {
while (left >= 0 && right < s.size() && s[left] == s[right]) {
--left;
++right;
}
return {left + 1, right - 1};
}
string longestPalindrome(string s) {
int start = 0, end = 0;
for (int i = 0; i < s.size(); ++i) {
auto [left1, right1] = expandAroundCenter(s, i, i);
auto [left2, right2] = expandAroundCenter(s, i, i + 1);
if (right1 - left1 > end - start) {
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {
start = left2;
end = right2;
}
}
return s.substr(start, end - start + 1);
}
};
复杂度分析
- 时间复杂度:\(O(n^2)\),其中 \(n\) 是字符串的长度。
长度为 \(1\) 和 \(2\) 的回文中心分别有 \(n\) 和 \(n-1\) 个,每个回文中心最多会向外扩展 \(O(n)\) 次。
- 空间复杂度:\(O(1)\)。
方法三:\(\text{Manacher}\) 算法
还有一个复杂度为 \(O(n)\) 的 \(\text{Manacher}\) 算法
然而本算法十分复杂,一般不作为面试内容。
这里给出,仅供有兴趣的同学挑战自己。
为了表述方便,我们定义一个新概念臂长,表示中心扩展算法向外扩展的长度。
如果一个位置的最大回文字符串长度为 2 * length + 1 ,其臂长为 length。
下面的讨论只涉及长度为奇数的回文字符串。
长度为偶数的回文字符串我们将会在最后与长度为奇数的情况统一起来。
思路与算法
在中心扩展算法的过程中,我们能够得出每个位置的臂长。
那么当我们要得出以下一个位置 i 的臂长时,能不能利用之前得到的信息呢?答案是肯定的。
具体来说,如果位置 j 的臂长为 length,并且有 j + length > i,如下图所示: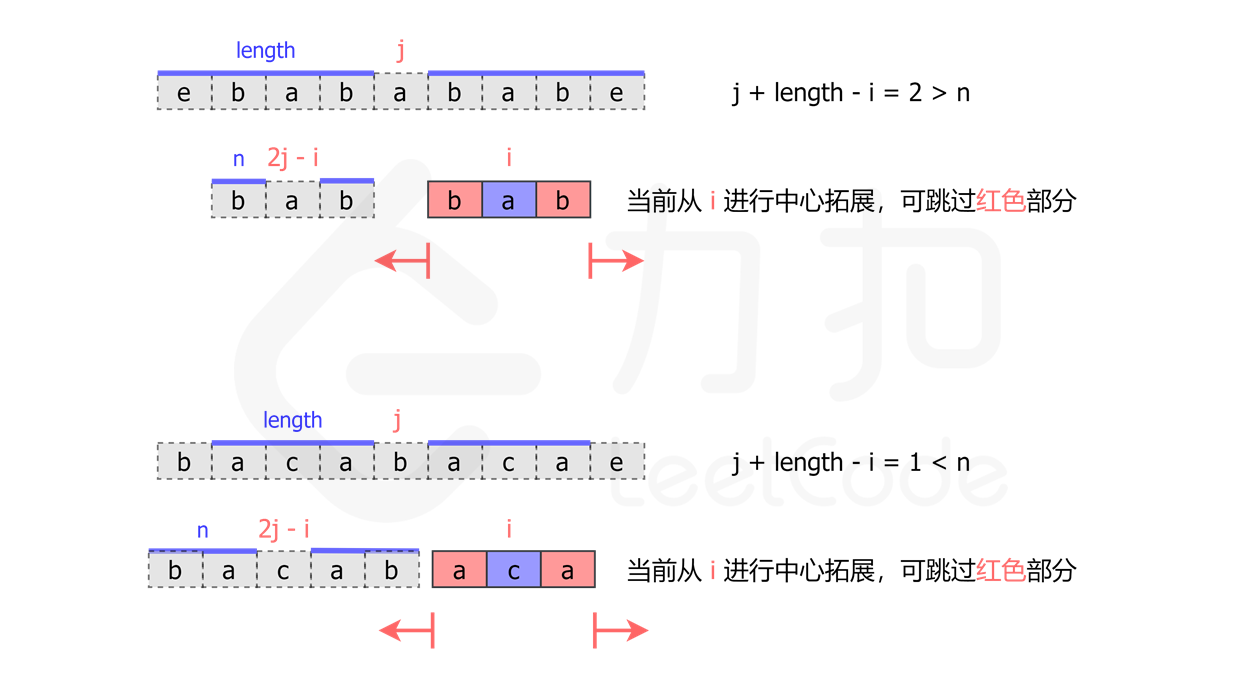 当在位置
当在位置 i 开始进行中心拓展时,我们可以先找到 i 关于 j 的对称点 2 * j - i。
那么如果点 2 * j - i 的臂长等于 n,我们就可以知道,点 i 的臂长至少为 min(j + length - i, n)。
那么我们就可以直接跳过 i 到 i + min(j + length - i, n) 这部分,从 i + min(j + length - i, n) + 1 开始拓展。
我们只需要在中心扩展法的过程中记录右臂在最右边的回文字符串,将其中心作为 j,在计算过程中就能最大限度地避免重复计算。
那么现在还有一个问题:如何处理长度为偶数的回文字符串呢?我们可以通过一个特别的操作将奇偶数的情况统一起来:我们向字符串的头尾以及每两个字符中间添加一个特殊字符 #,比如字符串 aaba 处理后会变成 #a#a#b#a#。
那么原先长度为偶数的回文字符串 aa 会变成长度为奇数的回文字符串 #a#a#,而长度为奇数的回文字符串 aba 会变成长度仍然为奇数的回文字符串 #a#b#a#,我们就不需要再考虑长度为偶数的回文字符串了。
注意这里的特殊字符不需要是没有出现过的字母,我们可以使用任何一个字符来作为这个特殊字符。
这是因为,当我们只考虑长度为奇数的回文字符串时,每次我们比较的两个字符奇偶性一定是相同的,所以原来字符串中的字符不会与插入的特殊字符互相比较,不会因此产生问题。
class Solution {
public:
int expand(const string& s, int left, int right) {
while (left >= 0 && right < s.size() && s[left] == s[right]) {
--left;
++right;
}
return (right - left - 2) / 2;
}
string longestPalindrome(string s) {
int start = 0, end = -1;
string t = "#";
for (char c: s) {
t += c;
t += '#';
}
t += '#';
s = t;
vector<int> arm_len;
int right = -1, j = -1;
for (int i = 0; i < s.size(); ++i) {
int cur_arm_len;
if (right >= i) {
int i_sym = j * 2 - i;
int min_arm_len = min(arm_len[i_sym], right - i);
cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);
} else {
cur_arm_len = expand(s, i, i);
}
arm_len.push_back(cur_arm_len);
if (i + cur_arm_len > right) {
j = i;
right = i + cur_arm_len;
}
if (cur_arm_len * 2 + 1 > end - start) {
start = i - cur_arm_len;
end = i + cur_arm_len;
}
}
string ans;
for (int i = start; i <= end; ++i) {
if (s[i] != '#') {
ans += s[i];
}
}
return ans;
}
};
复杂度分析
- 时间复杂度:\(O(n)\),其中 \(n\) 是字符串的长度。
由于对于每个位置,扩展要么从当前的最右侧臂长 right 开始,要么只会进行一步,而 right 最多向前走 \(O(n)\) 步,因此算法的复杂度为 \(O(n)\)。
- 空间复杂度:\(O(n)\),我们需要 \(O(n)\) 的空间记录每个位置的臂长