azarasi / LeetCode 84. 柱状图中最大的矩形

给定 n个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

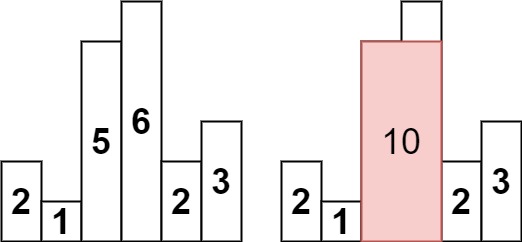
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

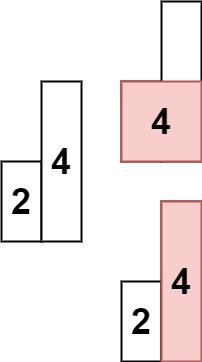
输入： heights = [2,4]
输出： 4

提示：

• \(1 <= heights.length <=10^5\)
• \(0 <= heights[i] <= 10^4\)

题解

前言

我们需要在柱状图中找出最大的矩形，因此我们可以考虑枚举矩形的宽和高，其中「宽」表示矩形贴着柱状图底边的宽度，「高」表示矩形在柱状图上的高度。

• 如果我们枚举「宽」，我们可以使用两重循环枚举矩形的左右边界以固定宽度 \(w\)，此时矩形的高度 \(h\)，就是所有包含在内的柱子的「最小高度」，对应的面积为 \(w \times h\)。下面给出了这种方法的 C++ 代码。

  class Solution {
  public:
      int largestRectangleArea(vector<int>& heights) {
          int n = heights.size();
          int ans = 0;
          // 枚举左边界
          for (int left = 0; left < n; ++left) {
              int minHeight = INT_MAX;
              // 枚举右边界
              for (int right = left; right < n; ++right) {
                  // 确定高度
                  minHeight = min(minHeight, heights[right]);
                  // 计算面积
                  ans = max(ans, (right - left + 1) * minHeight);
              }
          }
          return ans;
      }
  };
  

• 如果我们枚举「高」，我们可以使用一重循环枚举某一根柱子，将其固定为矩形的高度 \(h\)。随后我们从这跟柱子开始向两侧延伸，直到遇到高度小于 \(h\) 的柱子，就确定了矩形的左右边界。如果左右边界之间的宽度为 \(w\)，那么对应的面积为 \(w \times h\)。下面给出了这种方法的 C++ 代码。

  class Solution {
  public:
      int largestRectangleArea(vector<int>& heights) {
          int n = heights.size();
          int ans = 0;
          for (int mid = 0; mid < n; ++mid) {
              // 枚举高
              int height = heights[mid];
              int left = mid, right = mid;
              // 确定左右边界
              while (left - 1 >= 0 && heights[left - 1] >= height) {
                  --left;
              }
              while (right + 1 < n && heights[right + 1] >= height) {
                  ++right;
              }
              // 计算面积
              ans = max(ans, (right - left + 1) * height);
          }
          return ans;
      }
  };
  

可以发现，这两种暴力方法的时间复杂度均为 \(O(N^2)\)，会超出时间限制，我们必须要进行优化。考虑到枚举「宽」的方法使用了两重循环，本身就已经需要 \(O(N^2)\) 的时间复杂度，不容易优化，因此我们可以考虑优化只使用了一重循环的枚举「高」的方法。

方法一：单调栈

思路

我们归纳一下枚举「高」的方法：

• 首先我们枚举某一根柱子 \(i\) 作为高 \(h = \textit{heights}[i]\)；

• 随后我们需要进行向左右两边扩展，使得扩展到的柱子的高度均不小于 \(h\)。换句话说，我们需要找到左右两侧最近的高度小于 \(h\) 的柱子，这样这两根柱子之间（不包括其本身）的所有柱子高度均不小于 \(h\)，并且就是 \(i\) 能够扩展到的最远范围。

那么我们先来看看如何求出一根柱子的左侧且最近的小于其高度的柱子。除了根据「前言」部分暴力地进行枚举之外，我们可以通过如下的一个结论来深入地进行思考：

对于两根柱子 \(j_0\) 以及 \(j_1\)，如果 \(j_0 < j_1\) 并且 \(\textit{heights}[j_0] \geq \textit{heights}[j_1]\)，那么对于任意的在它们之后出现的柱子 \(i\)（\(j_1 < i\)），\(j_0\) 一定不会是 \(i\) 左侧且最近的小于其高度的柱子。

换句话说，如果有两根柱子 \(j_0\) 和 \(j_1\)，其中 \(j_0\) 在 \(j_1\) 的左侧，并且 \(j_0\) 的高度大于等于 \(j_1\)，那么在后面的柱子 \(i\) 向左找小于其高度的柱子时，\(j_1\) 会「挡住」\(j_0\)，\(j_0\) 就不会作为答案了。

这样以来，我们可以对数组从左向右进行遍历，同时维护一个「可能作为答案」的数据结构，其中按照从小到大的顺序存放了一些 \(j\) 值。根据上面的结论，如果我们存放了 \(j_0, j_1, \cdots, j_s\)，那么一定有 \(\textit{height}[j_0] < \textit{height}[j_1] < \cdots < \textit{height}[j_s]\)，因为如果有两个相邻的 \(j\) 值对应的高度不满足 \(<\) 关系，那么后者会「挡住」前者，前者就不可能作为答案了。

当我们枚举到第 \(i\) 根柱子时，我们的数据结构中存放了 \(j_0, j_1, \cdots, j_s\)，如果第 \(i\) 根柱子左侧且最近的小于其高度的柱子为 \(j_i\)，那么必然有

$$ \textit{height}[j_0] < \textit{height}[j_1] < \cdots < \textit{height}[j_i] < \textit{height}[i] \leq \textit{height}[j_{i+1}] < \cdots < \textit{height}[j_s] $$

这样我们就可以使用二分查找的方法找到 \(i\) 对应的 \(j_i\)，但真的需要吗？当我们枚举到 \(i+1\) 时，原来的 \(i\) 也变成了 \(j\) 值，因此 \(i\) 会被放入数据结构。由于所有在数据结构中的 \(j\) 值均小于 \(i\)，那么所有高度大于等于 \(\textit{height}[i]\) 的 \(j\) 都不会作为答案，需要从数据结构中移除。而我们发现，这些被移除的 \(j\) 值恰好就是

$$ j_{i+1}, \cdots, j_s $$

这样我们在枚举到第 \(i\) 根柱子的时候，就可以先把所有高度大于等于 \(\textit{height}[i]\) 的 \(j\) 值全部移除，剩下的 \(j\) 值中高度最高的即为答案。在这之后，我们将 \(i\) 放入数据结构中，开始接下来的枚举。此时，我们需要使用的数据结构也就呼之欲出了，它就是栈。

• 栈中存放了 \(j\) 值。从栈底到栈顶，\(j\) 的值严格单调递增，同时对应的高度值也严格单调递增；

• 当我们枚举到第 \(i\) 根柱子时，我们从栈顶不断地移除 \(\textit{height}[j] \geq \textit{height}[i]\) 的 \(j\) 值。在移除完毕后，栈顶的 \(j\) 值就一定满足 \(\textit{height}[j] < \textit{height}[i]\)，此时 \(j\) 就是 \(i\) 左侧且最近的小于其高度的柱子。

  • 这里会有一种特殊情况。如果我们移除了栈中所有的 \(j\) 值，那就说明 \(i\) 左侧所有柱子的高度都大于 \(\textit{height}[i]\)，那么我们可以认为 \(i\) 左侧且最近的小于其高度的柱子在位置 \(j=-1\)，它是一根「虚拟」的、高度无限低的柱子。这样的定义不会对我们的答案产生任何的影响，我们也称这根「虚拟」的柱子为「哨兵」。

• 我们再将 \(i\) 放入栈顶。

栈中存放的元素具有单调性，这就是经典的数据结构「单调栈」了。

例子

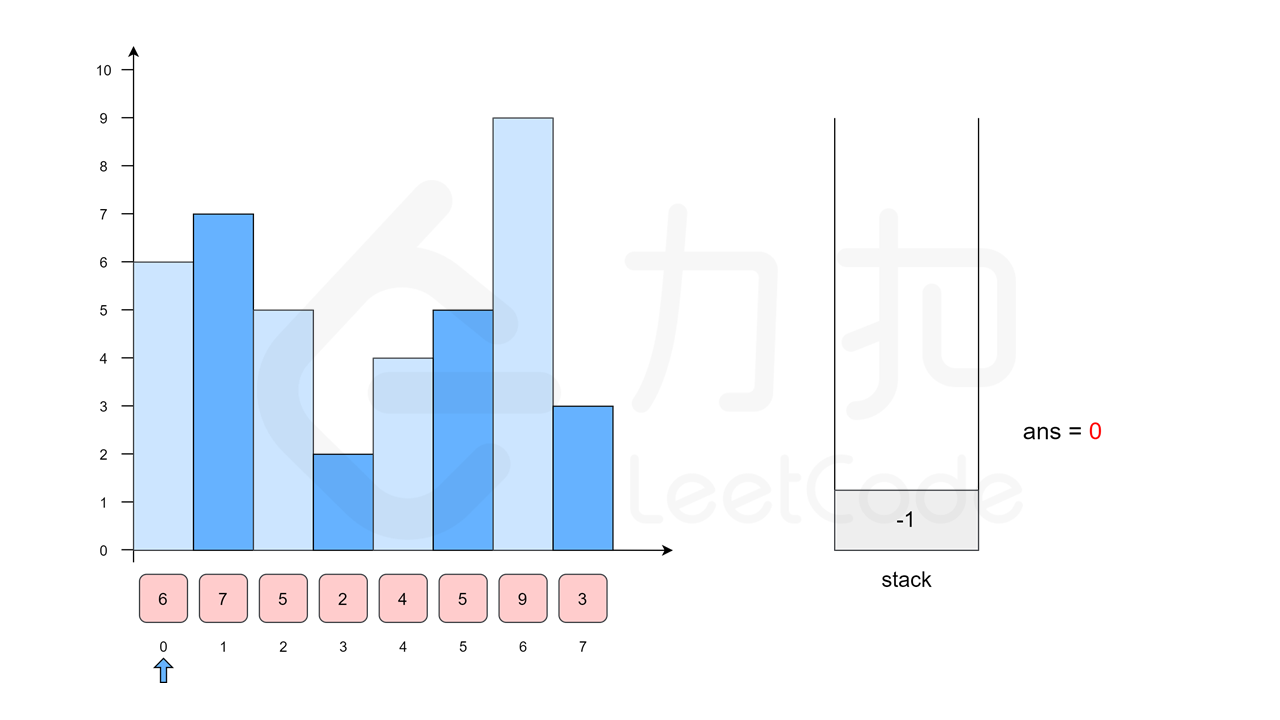
我们用一个具体的例子 \([6, 7, 5, 2, 4, 5, 9, 3]\) 来帮助读者理解单调栈。我们需要求出每一根柱子的左侧且最近的小于其高度的柱子。初始时的栈为空。

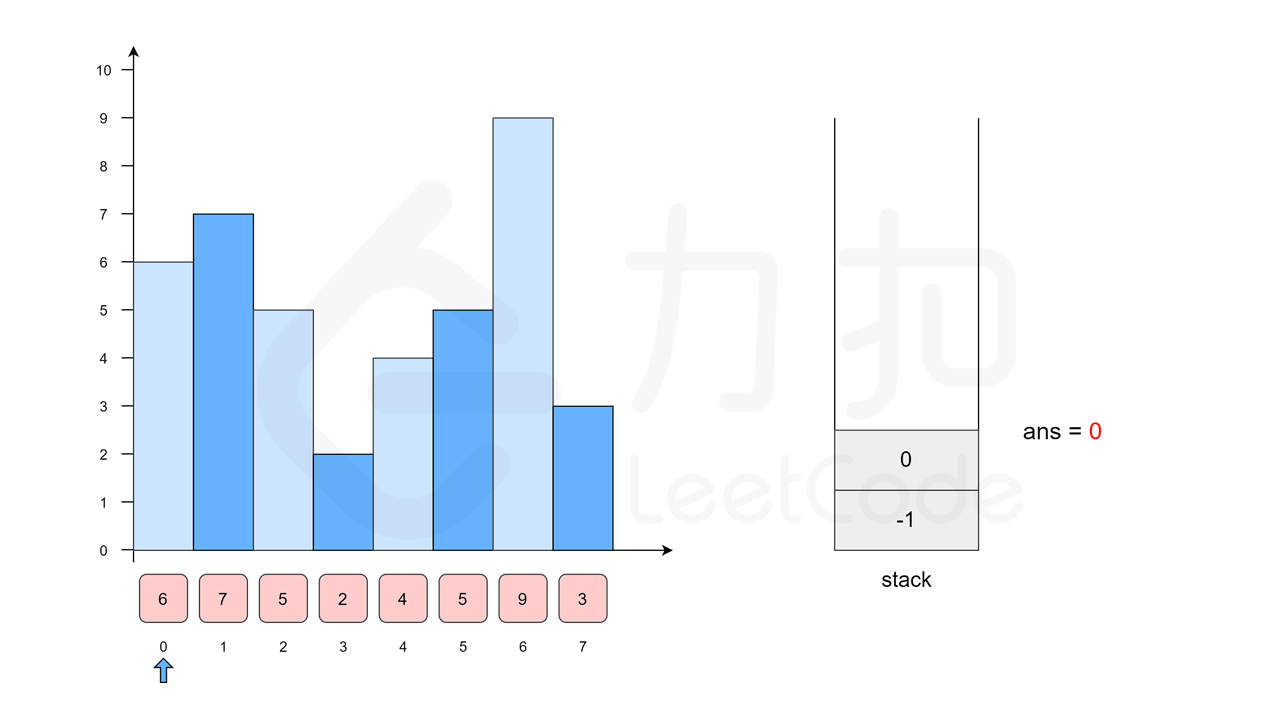
• 我们枚举 \(6\)，因为栈为空，所以 \(6\) 左侧的柱子是「哨兵」，位置为 -1。随后我们将 \(6\) 入栈。

  • 栈：[6(0)]。（这里括号内的数字表示柱子在原数组中的位置）

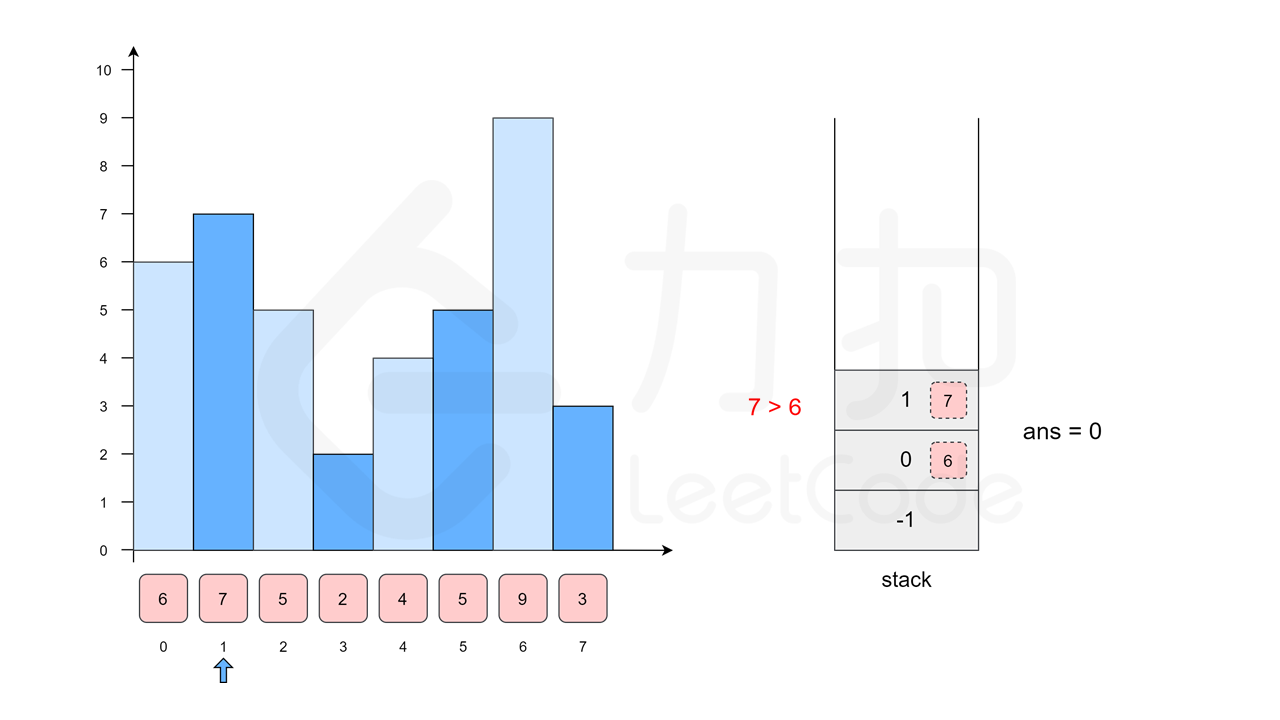
• 我们枚举 \(7\)，由于 \(6<7\)，因此不会移除栈顶元素，所以 \(7\) 左侧的柱子是 \(6\)，位置为 \(0\)。随后我们将 \(7\) 入栈。

  • 栈：[6(0), 7(1)]

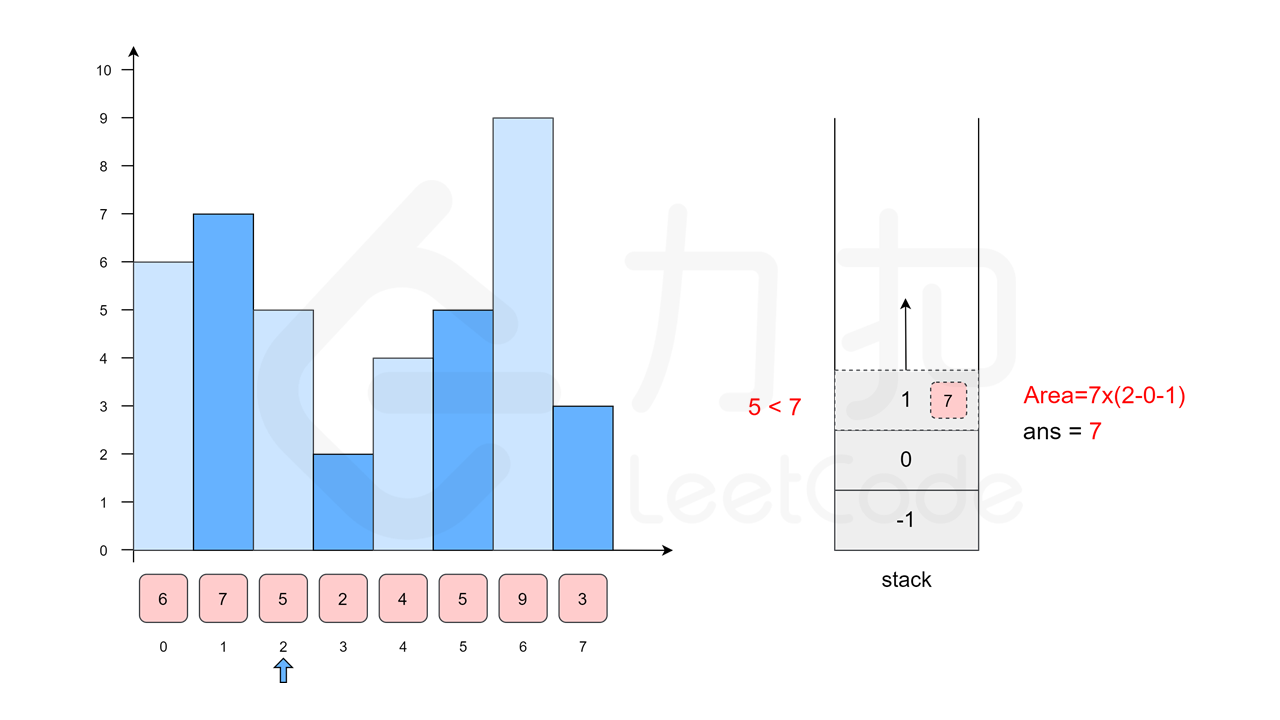
• 我们枚举 \(5\)，由于 \(7\geq 5\)，因此移除栈顶元素 \(7\)。同样地，\(6 \geq 5\)，再移除栈顶元素 \(6\)。此时栈为空，所以 \(5\) 左侧的柱子是「哨兵」，位置为 \(-1\)。随后我们将 \(5\) 入栈。

  • 栈：[5(2)]

• 接下来的枚举过程也大同小异。我们枚举 \(2\)，移除栈顶元素 \(5\)，得到 \(2\) 左侧的柱子是「哨兵」，位置为 \(-1\)。将 \(2\) 入栈。

  • 栈：[2(3)]

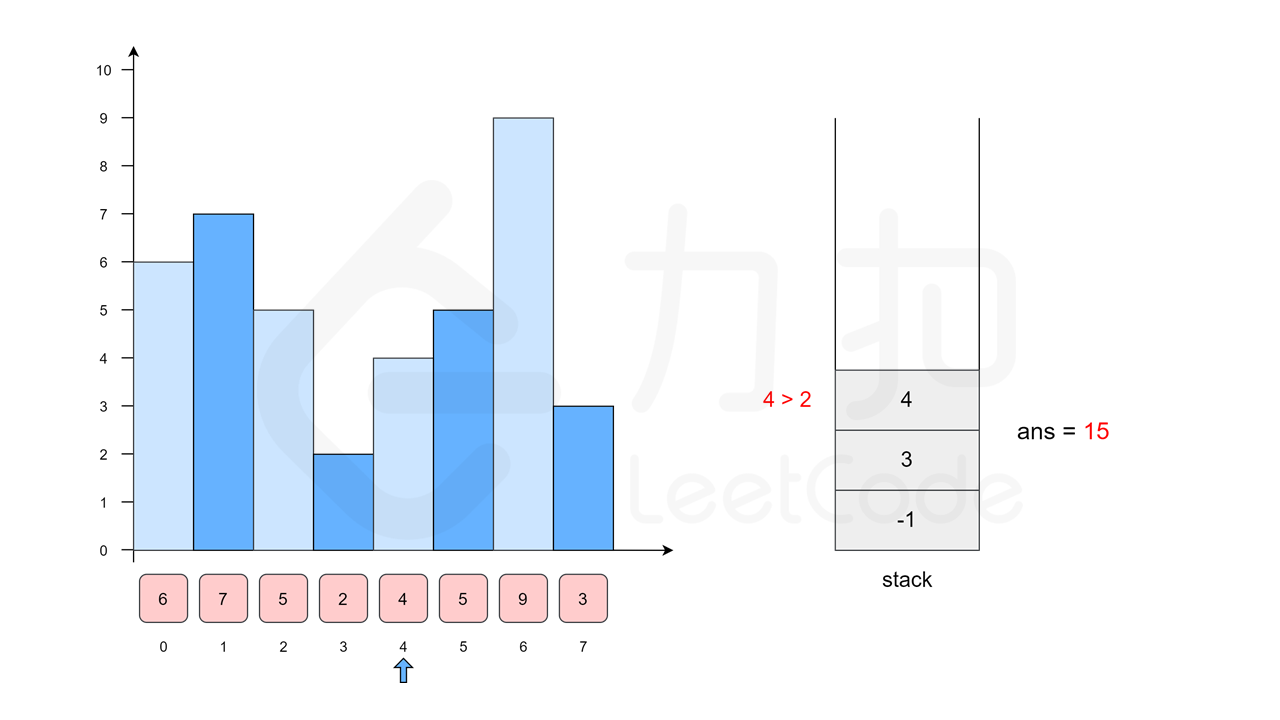
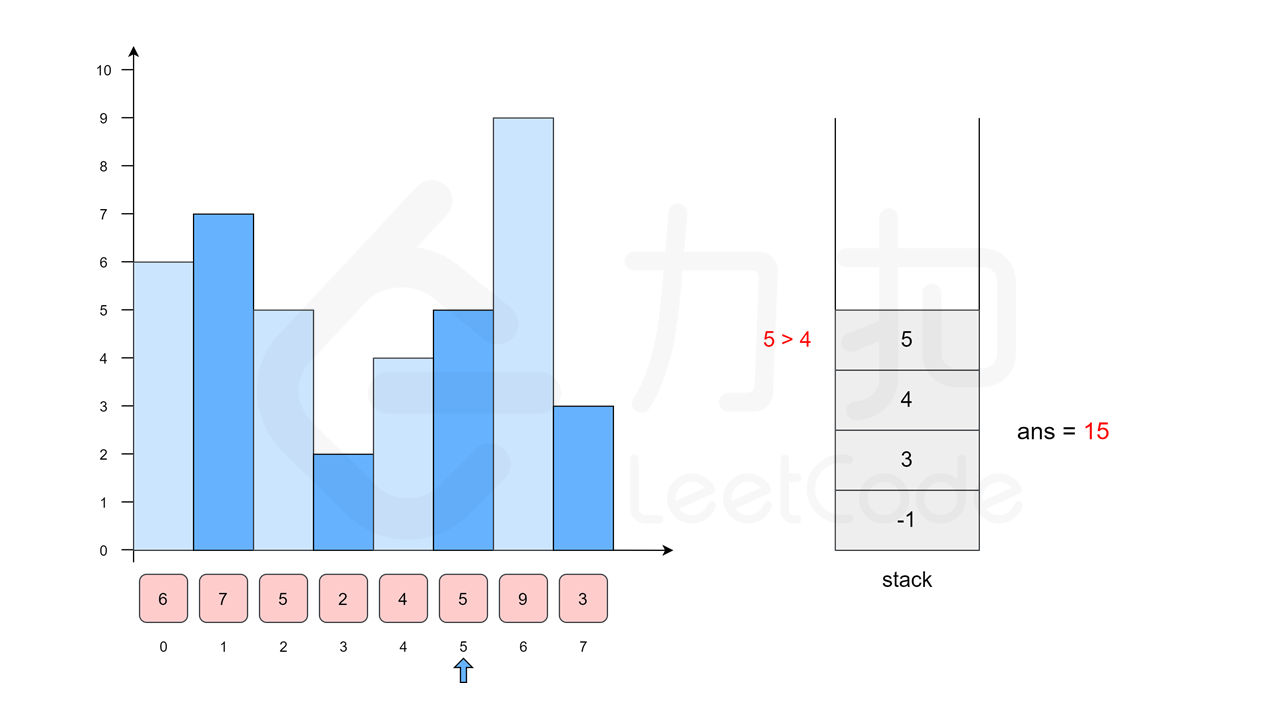
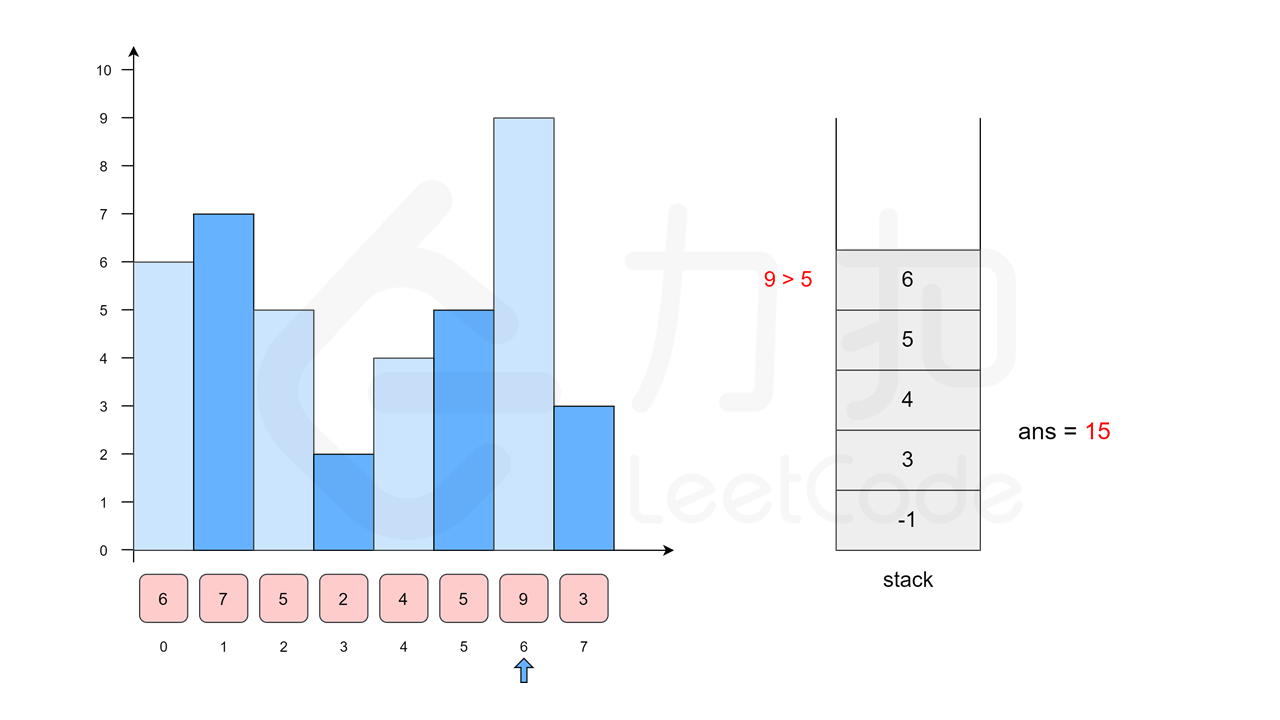
• 我们枚举 \(4\)，\(5\) 和 \(9\)，都不会移除任何栈顶元素，得到它们左侧的柱子分别是 \(2\)，\(4\) 和 \(5\)，位置分别为 \(3\)，\(4\) 和 \(5\)。将它们入栈。

  • 栈：[2(3), 4(4), 5(5), 9(6)]

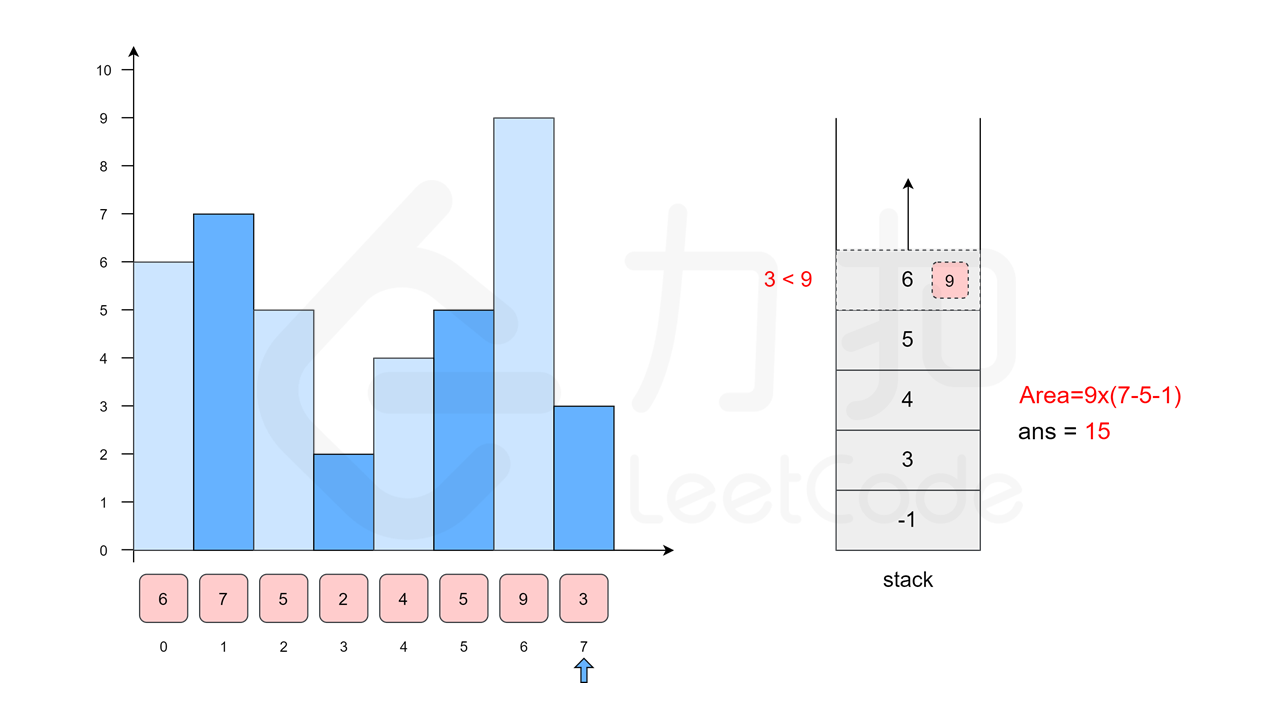
• 我们枚举 \(3\)，依次移除栈顶元素 \(9\)，\(5\) 和 \(4\)，得到 \(3\) 左侧的柱子是 \(2\)，位置为 \(3\)。将 \(3\) 入栈。

  • 栈：[2(3), 3(7)]

这样以来，我们得到它们左侧的柱子编号分别为 \([-1, 0, -1, -1, 3, 4, 5, 3]\)。用相同的方法，我们从右向左进行遍历，也可以得到它们右侧的柱子编号分别为 \([2, 2, 3, 8, 7, 7, 7, 8]\)，这里我们将位置 \(8\) 看作「哨兵」。

在得到了左右两侧的柱子之后，我们就可以计算出每根柱子对应的左右边界，并求出答案了。

分析

单调栈的时间复杂度是多少？直接计算十分困难，但是我们可以发现：

每一个位置只会入栈一次（在枚举到它时），并且最多出栈一次。

因此当我们从左向右/总右向左遍历数组时，对栈的操作的次数就为 \(O(N)\)。所以单调栈的总时间复杂度为 \(O(N)\)。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];

        Deque<Integer> mono_stack = new ArrayDeque<Integer>();
        for (int i = 0; i < n; ++i) {
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                mono_stack.pop();
            }
            left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
            mono_stack.push(i);
        }

        mono_stack.clear();
        for (int i = n - 1; i >= 0; --i) {
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                mono_stack.pop();
            }
            right[i] = (mono_stack.isEmpty() ? n : mono_stack.peek());
            mono_stack.push(i);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：\(O(N)\)。

• 空间复杂度：\(O(N)\)。

方法二：单调栈 + 常数优化

在方法一中，我们首先从左往右对数组进行遍历，借助单调栈求出了每根柱子的左边界，随后从右往左对数组进行遍历，借助单调栈求出了每根柱子的右边界。那么我们是否可以只遍历一次就求出答案呢？

答案是可以的。在方法一中，我们在对位置 \(i\) 进行入栈操作时，确定了它的左边界。从直觉上来说，与之对应的我们在对位置 \(i\) 进行出栈操作时可以确定它的右边界！仔细想一想，这确实是对的。当位置 \(i\) 被弹出栈时，说明此时遍历到的位置 \(i_0\) 的高度小于等于 \(\textit{height}[i]\)，并且在 \(i_0\) 与 \(i\) 之间没有其他高度小于等于 \(\textit{height}[i]\) 的柱子。这是因为，如果在 \(i\) 和 \(i_0\) 之间还有其它位置的高度小于等于 \(\textit{height}[i]\) 的，那么在遍历到那个位置的时候，\(i\) 应该已经被弹出栈了。所以位置 \(i_0\) 就是位置 \(i\) 的右边界。

等等，我们需要的是「一根柱子的左侧且最近的小于其高度的柱子」，但这里我们求的是小于等于，那么会造成什么影响呢？答案是：我们确实无法求出正确的右边界，但对最终的答案没有任何影响。这是因为在答案对应的矩形中，如果有若干个柱子的高度都等于矩形的高度，那么最右侧的那根柱子是可以求出正确的右边界的，而我们没有对求出左边界的算法进行任何改动，因此最终的答案还是可以从最右侧的与矩形高度相同的柱子求得的。读者可以仔细思考一下这一步。

在遍历结束后，栈中仍然有一些位置，这些位置对应的右边界就是位置为 \(n\) 的「哨兵」。我们可以将它们依次出栈并更新右边界，也可以在初始化右边界数组时就将所有的元素的值置为 \(n\)。

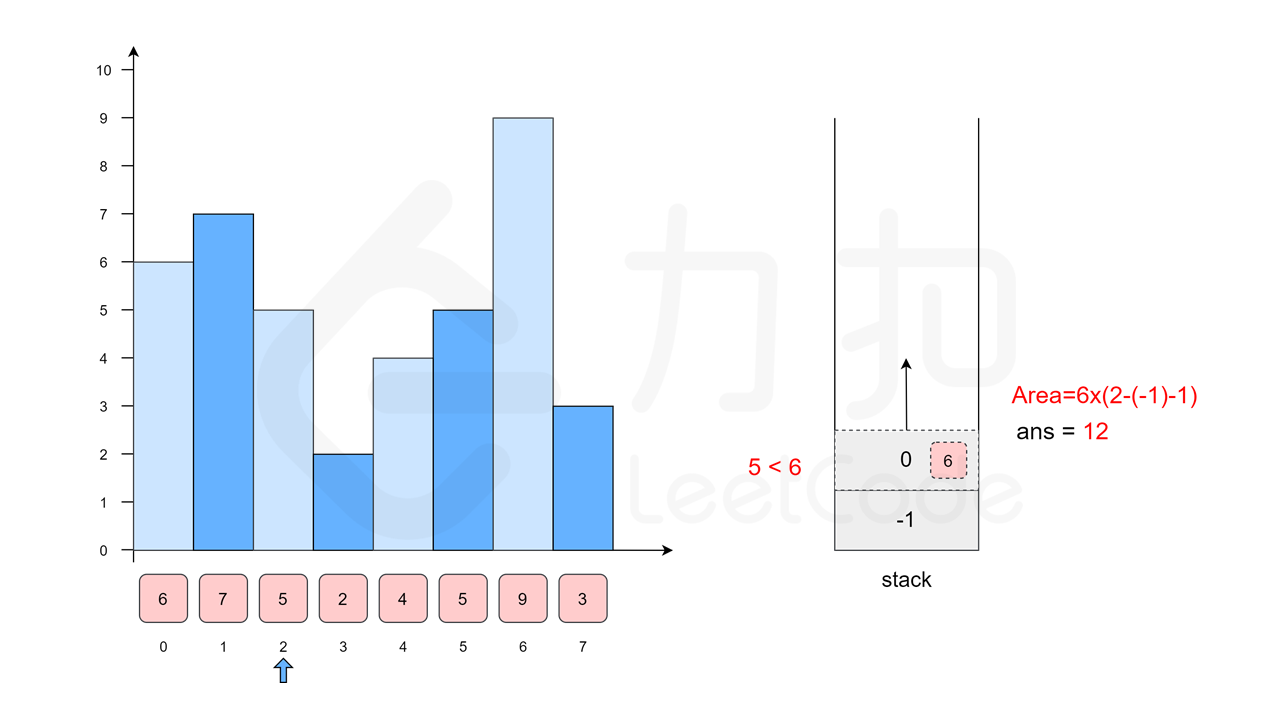
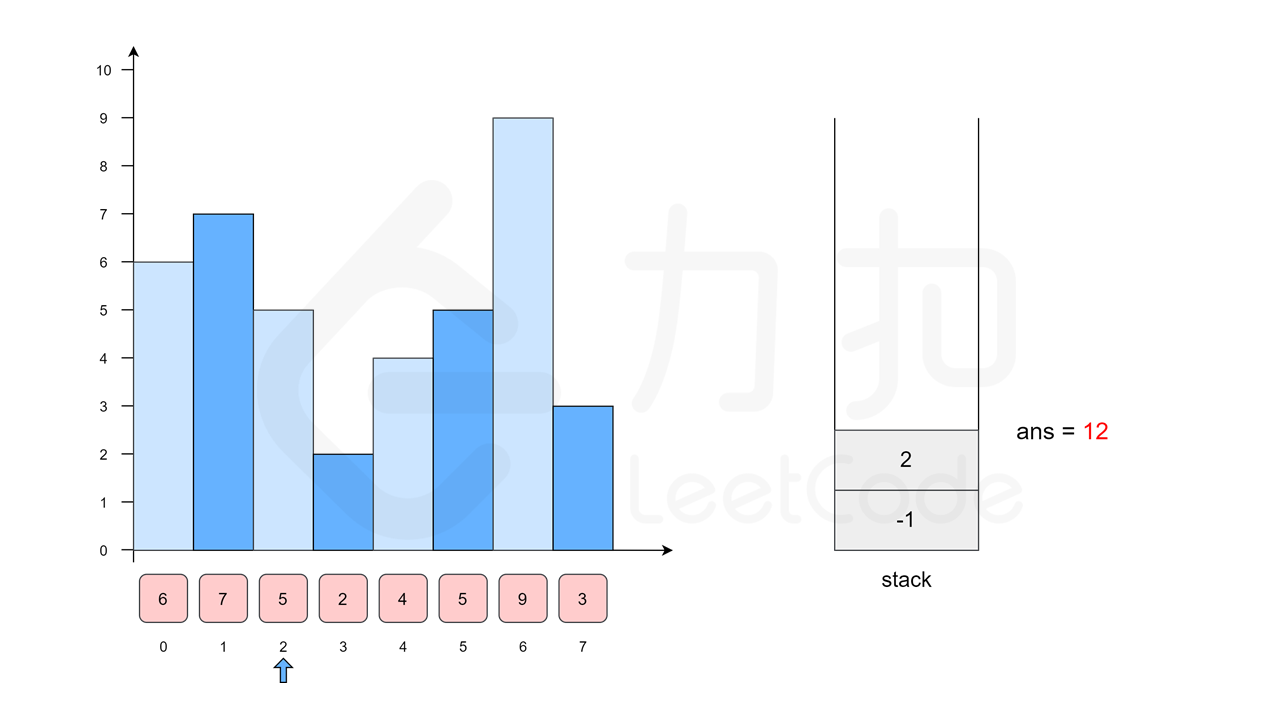
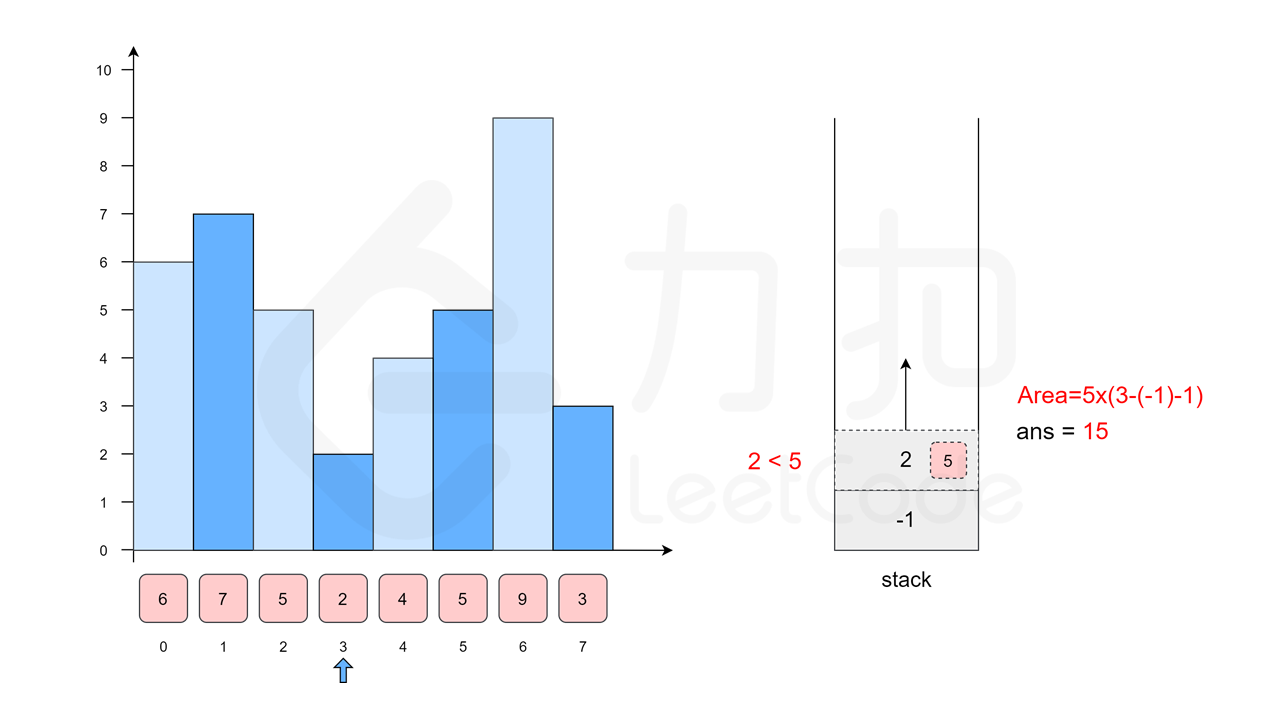
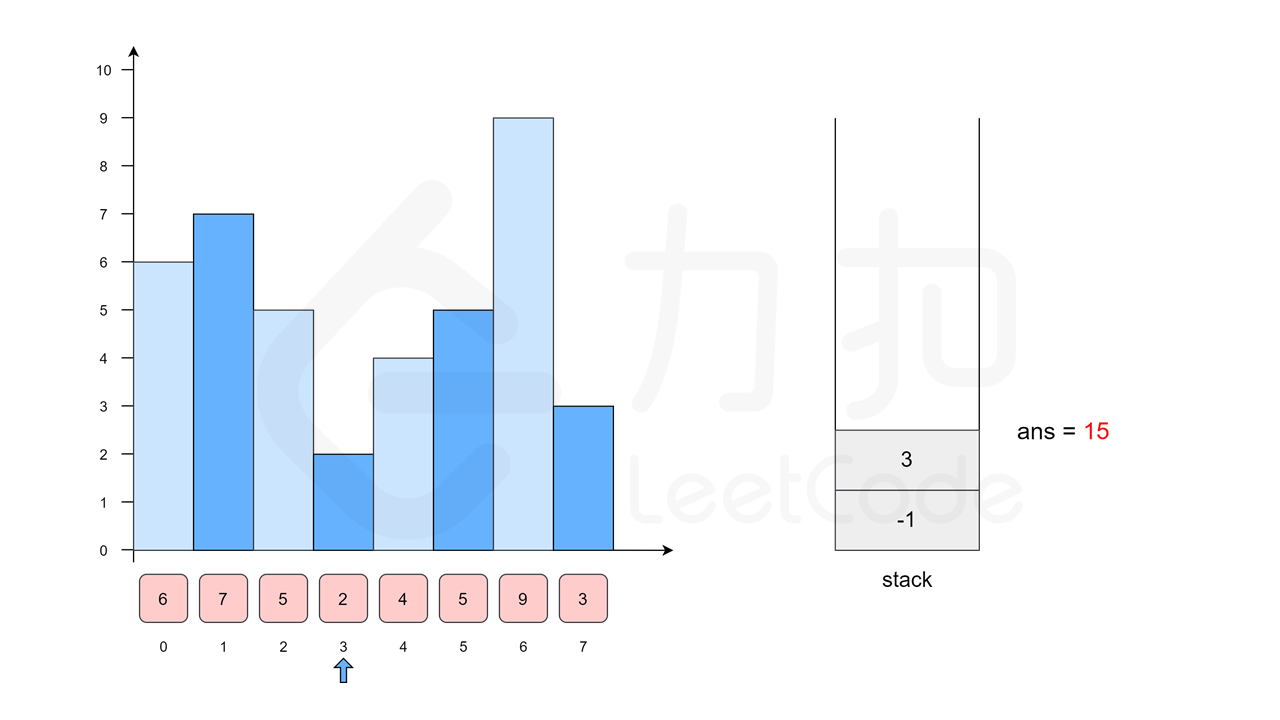
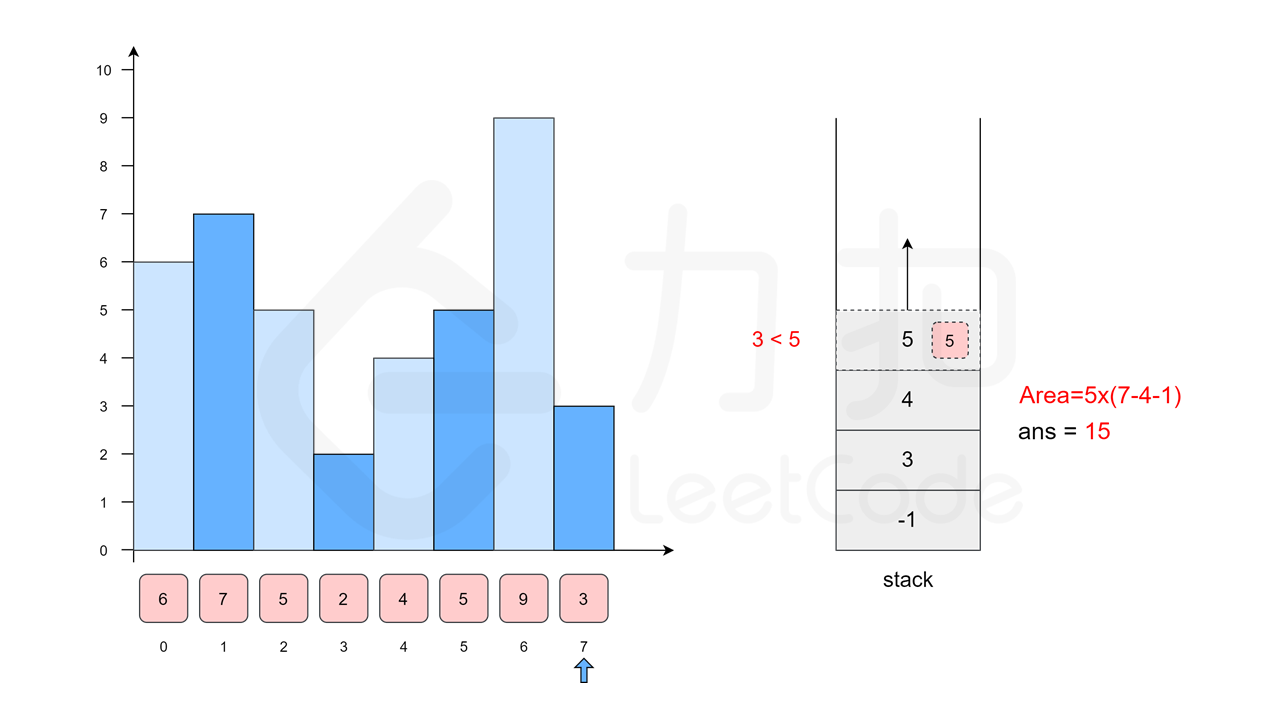
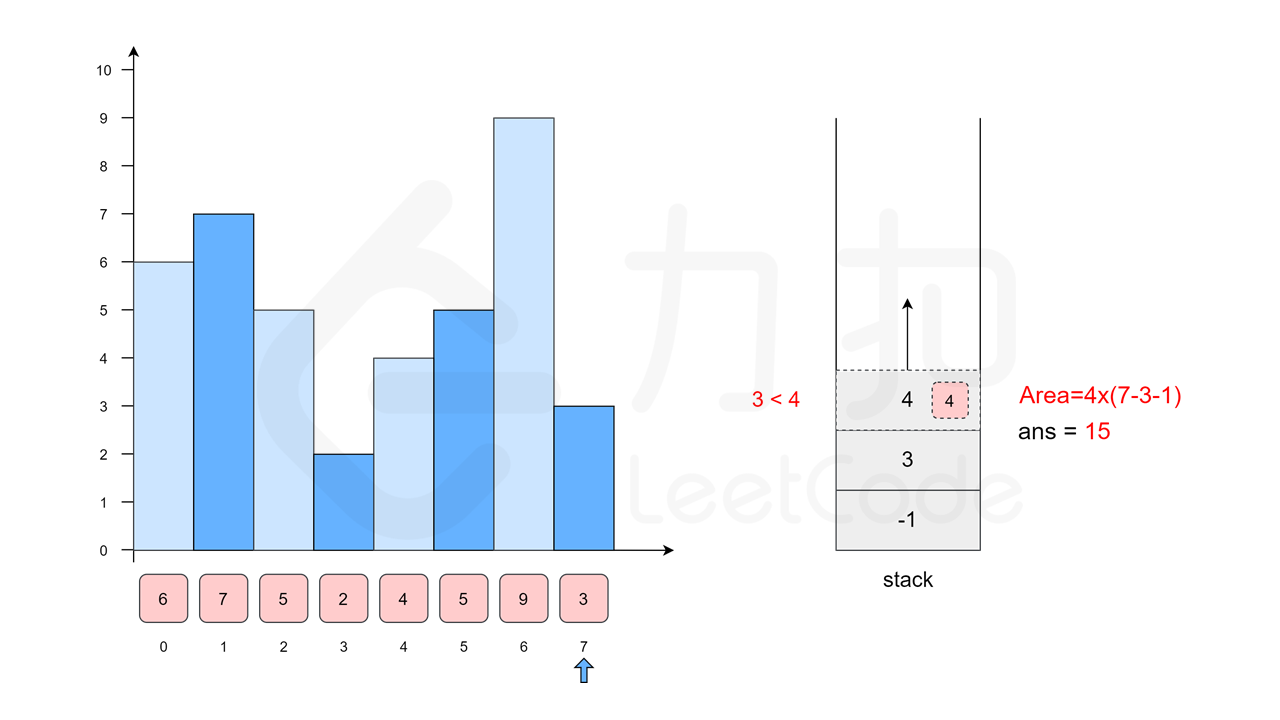
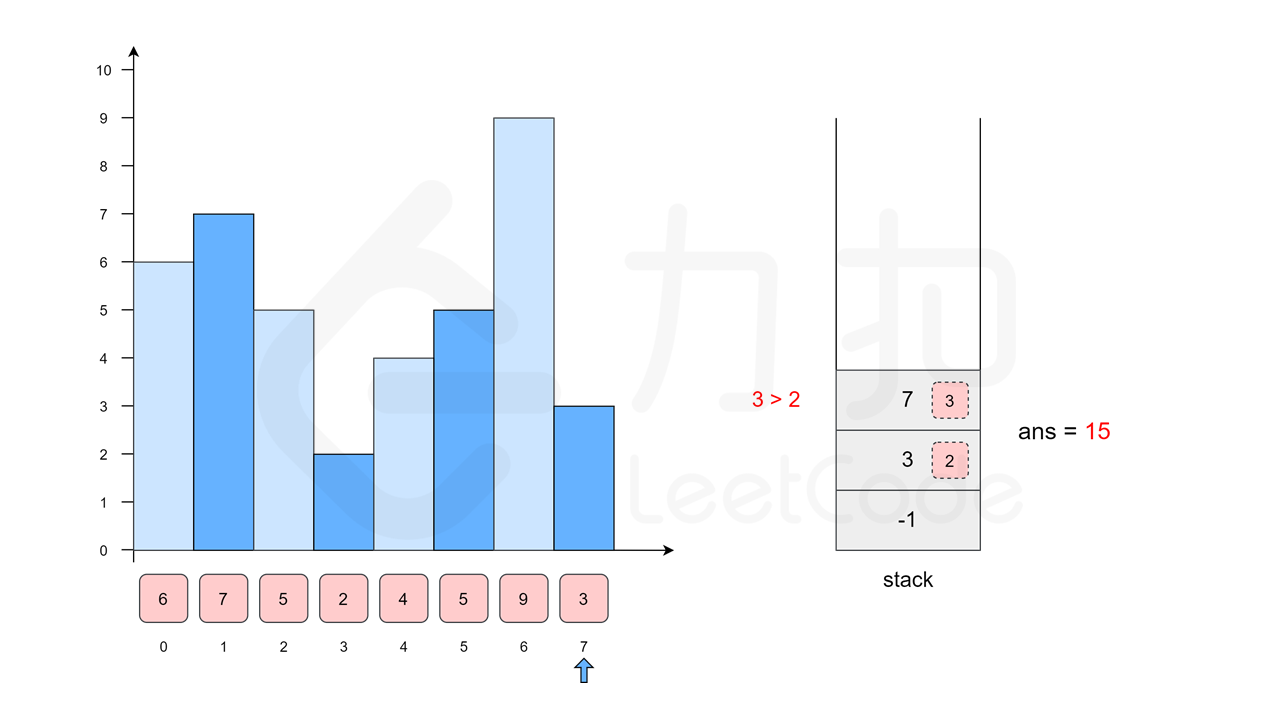
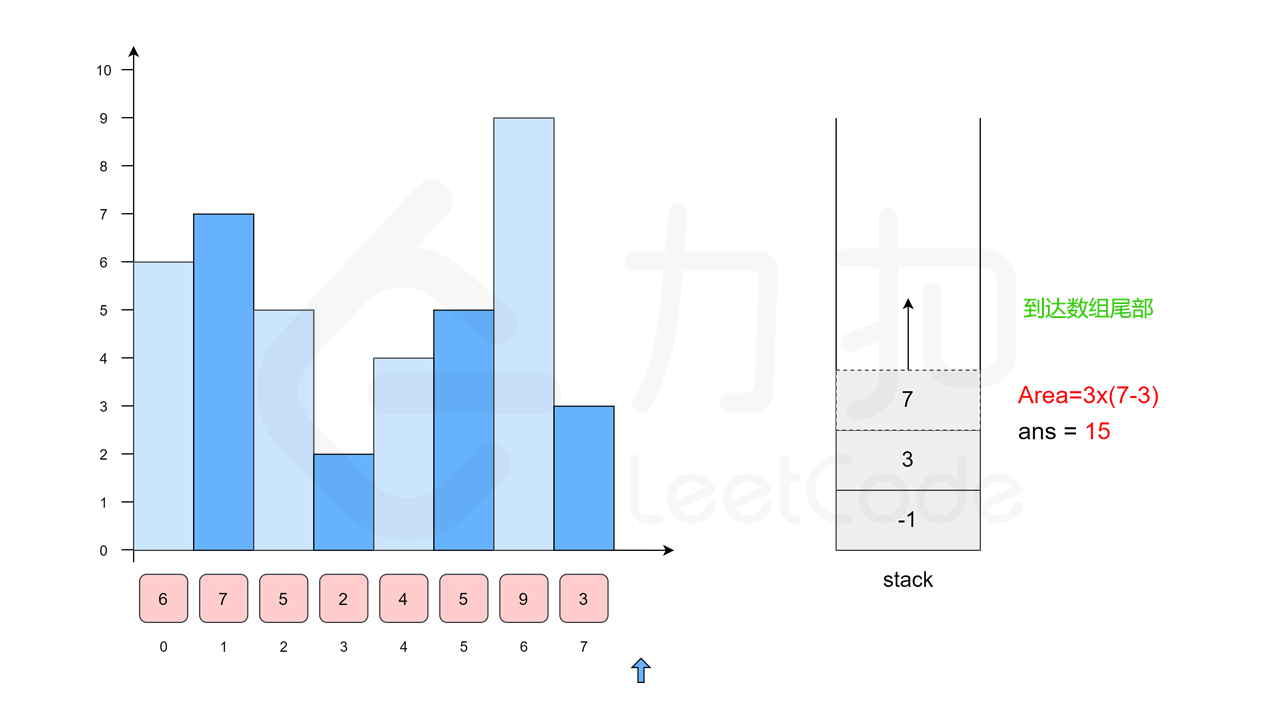
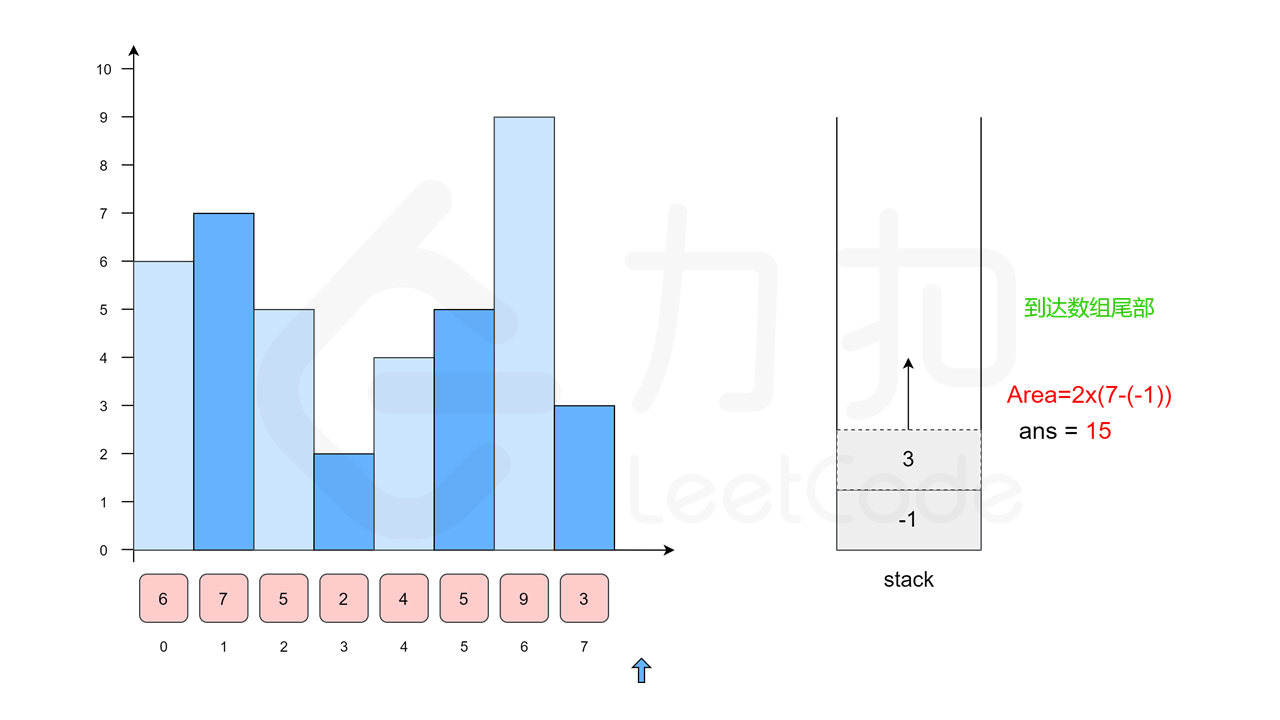
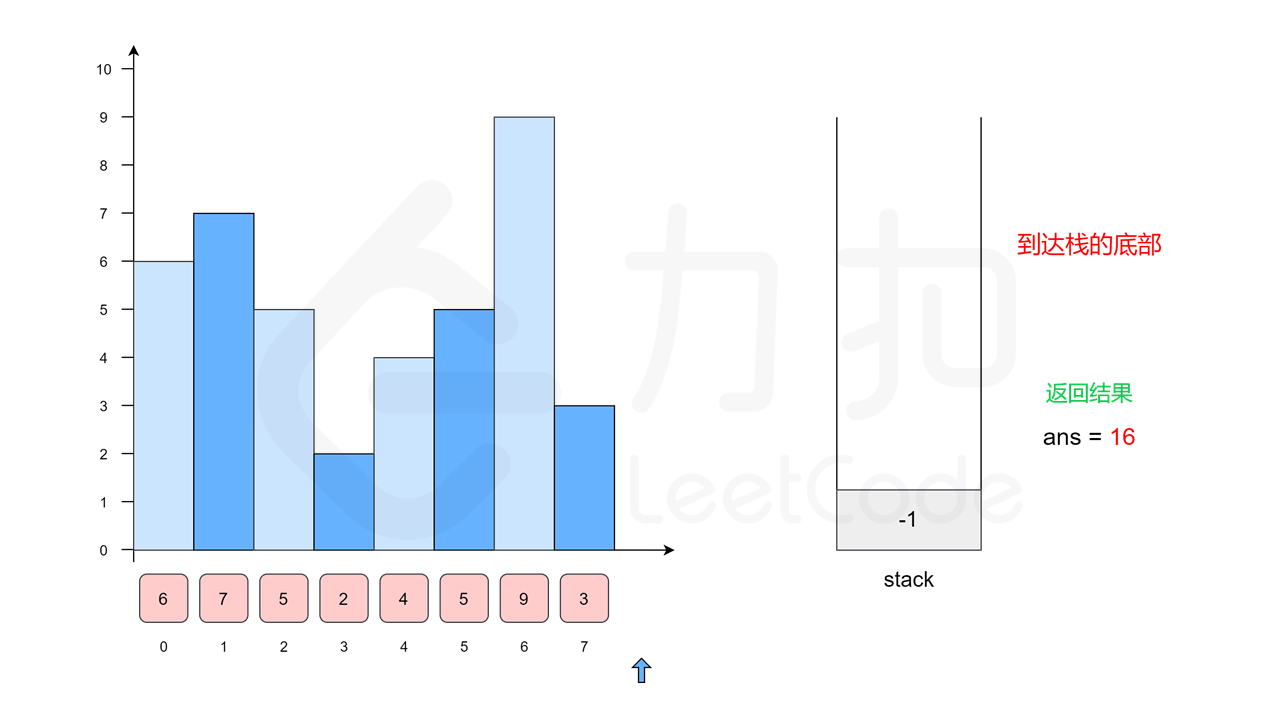
我们沿用方法一中的例子 \([6, 7, 5, 2, 4, 5, 9, 3]\)，下面的幻灯片给出了优化后的流程。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);

        Deque<Integer> mono_stack = new ArrayDeque<Integer>();
        for (int i = 0; i < n; ++i) {
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                right[mono_stack.peek()] = i;
                mono_stack.pop();
            }
            left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
            mono_stack.push(i);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：\(O(N)\)。

• 空间复杂度：\(O(N)\)。