Given two integers n and k, return the kth lexicographically smallest integer in the range [1, n].
Example 1:
Input: n = 13, k = 2
Output: 10
Explanation: The lexicographical order is [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9], so the second smallest number is 10.
Example 2:
Input: n = 1, k = 1
Output: 1
Constraints:
- \(1 <= k <= n <= 10^9\)
题解
题目要求找到字典序第 k 小的数字,可以将所有的数字都转换成字符串,然后排序找到第 k 小的数字即可,但显然时间复杂度不符合要求。我们利用字典树的特性将所有小于等于 n 的数字按照字典序的方式进行重建,可以得到如下:
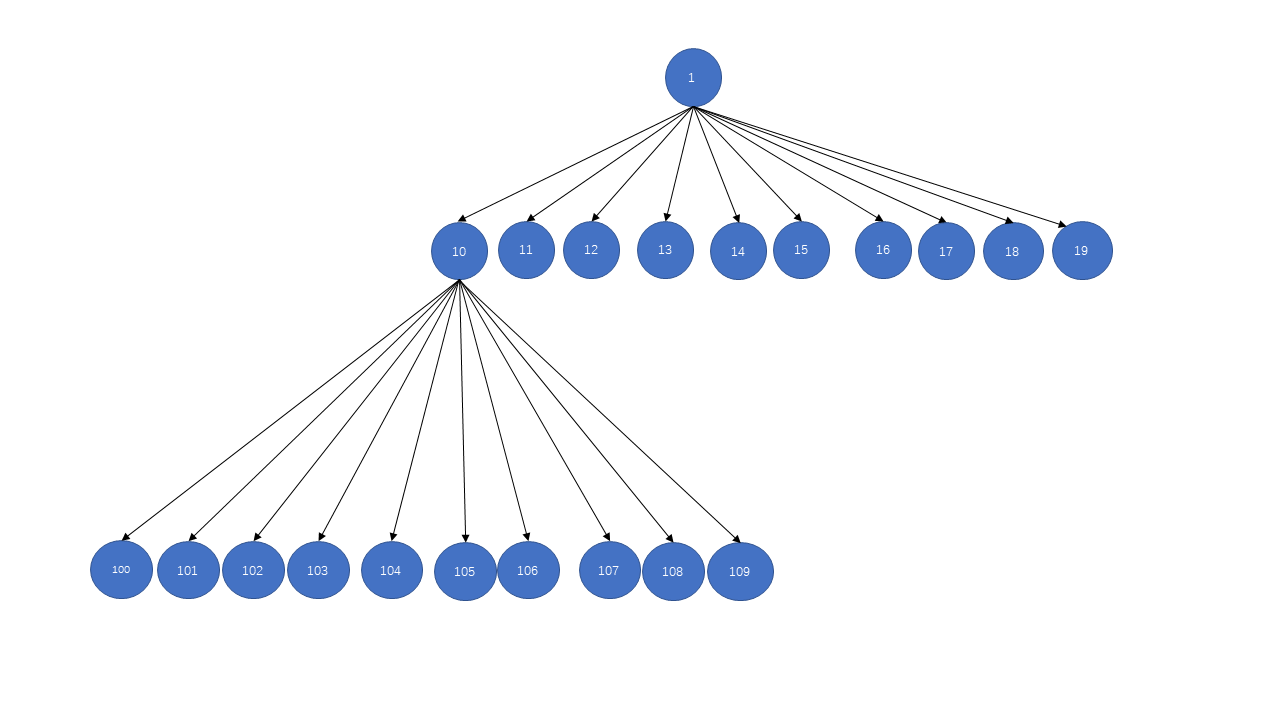
通过观察可以发现,前序遍历该字典树即可得到字典序从小到大的数字序列,遍历到第 k 个节点即为第 k 小的数字。我们可以构造字典树,并通过前序遍历求得目标节点,时间复杂度为 O(k)。实际不需要构造字典树,已知节点 i 的子节点为 (10×i,10×i+1,⋯,10×i+9),可以通过计算找到前序遍历第 k 个节点即可。设当前的字典树的第 i 小的节点为 \(n_i\),则只需按照先序遍历再继续往后找 k−i 个节点即为目标节点。设与 \(n_i\) 右侧相邻的兄弟节点为 \(n_{i+1}\),按照先序遍历的顺序,先访问 \(n_i\) 构造的子树,再访问 \(n_{i+1}\),此时满足 \(n_i < n_{i+1}\)。设以 \(n_i\) 为根节点构成的子树的节点数目为 \(step(n_i)\),则此时有以下两种可能:
如果满足 \(step(n_i)≤k−i\),则此时可以肯定第 k 小的节点一定不在 \(n_i\) 为根的子树中,存在于 \(n_i\) 的兄弟节点构成的子树中,则此时可以跳过 \(step(n_i)\) 个节点,从兄弟节点 \(n_{i+1}\) 开始往后查找 \(k−i−step(n_i)\) 个节点。
如果满足 \(step(n_i)>k−i\),则此时可以肯定第 k 小的节点一定在 \(n_i\) 构成的子树中,则此时需要在 \(n_i\) 的孩子节点中依次进行查找。此时跳过子树中最小的根节点 \(n_i\),从左侧第一个孩子开始往后查找 k−i−1 个节点,此时左侧第一个孩子的值为 \(10×ni_\)。
依次重复上述操作直到找到 k 小的节点即可。
在这里比较难以处理的是如何计算 \(step(n_i)\),即找到以 \(n_i\) 为根的子树下有多少节点。可以按照层次遍历子树,\(first_i\) 指向第 i 层的最左侧的孩子节点, \(last_i\) 指向第 i 层的最右侧的孩子节点,根据推理可以知道: \(first_i=10×first_{i−1}\),\(last_i=10×last_{i−1}+9\),第 i 层共有 \(last_i−first_{i+1}\) 个节点,由于所有的节点都需要满足小于等于 n,所以第 i 层的最右侧节点应该为 \(min(n,last_i)\),不断迭代直到 \(first_i>n\) 则终止向下搜索。实际上可以观察到最终结果一定是沿着字典树从根节点到某个叶子节点的路径进行搜索。
class Solution {
public:
int getSteps(int curr, long n) {
int steps = 0;
long first = curr;
long last = curr;
while (first <= n) {
steps += min(last, n) - first + 1;
first = first * 10;
last = last * 10 + 9;
}
return steps;
}
int findKthNumber(int n, int k) {
int curr = 1;
k--;
while (k > 0) {
int steps = getSteps(curr, n);
if (steps <= k) {
k -= steps;
curr++;
} else {
curr = curr*10;
k--;
}
}
return curr;
}
};