LeetCode 166. Fraction to Recurring Decimal - Harp Seal Pup Nursery and Caring Center

Given two integers representing the numerator and denominator of a fraction, return the fraction in string format.

If the fractional part is repeating, enclose the repeating part in parentheses.

If multiple answers are possible, return any of them.

It is guaranteed that the length of the answer string is less than 104 for all the given inputs.

Example 1:

Input: numerator = 1, denominator = 2
Output: "0.5"

Example 2:

Input: numerator = 2, denominator = 1
Output: "2"

Example 3:

Input: numerator = 4, denominator = 333
Output: "0.(012)"

Constraints:

\(-2^{31} <= numerator, denominator <= 2^{31} - 1\)
denominator != 0
No scary math, just apply elementary math knowledge. Still remember how to perform a long division?
Try a long division on 4/9, the repeating part is obvious. Now try 4/333. Do you see a pattern?
Notice that once the remainder starts repeating, so does the divided result.
Be wary of edge cases! List out as many test cases as you can think of and test your code thoroughly.

题解

题目要求根据给定的分子和分母，将分数转成整数或小数

由于给定的分子和分母的取值范围都是 \([-2^{31}, 2^{31}-1]\)，为了防止计算过程中产生溢出，需要将分子和分母转成 \(64\) 位整数表示。

将分数转成整数或小数，做法是计算分子和分母相除的结果。可能的结果有三种：整数、有限小数、无限循环小数。

如果分子可以被分母整除，则结果是整数，将分子除以分母的商以字符串的形式返回即可。

如果分子不能被分母整除，则结果是有限小数或无限循环小数，需要通过模拟长除法的方式计算结果。为了方便处理，首先根据分子和分母的正负决定结果的正负（注意此时分子和分母都不为 \(0\)），然后将分子和分母都转成正数，再计算长除法。

计算长除法时，首先计算结果的整数部分，将以下部分依次拼接到结果中

如果结果是负数则将负号拼接到结果中，如果结果是正数则跳过这一步；
将整数部分拼接到结果中；
将小数点拼接到结果中。

完成上述拼接之后，根据余数计算小数部分。

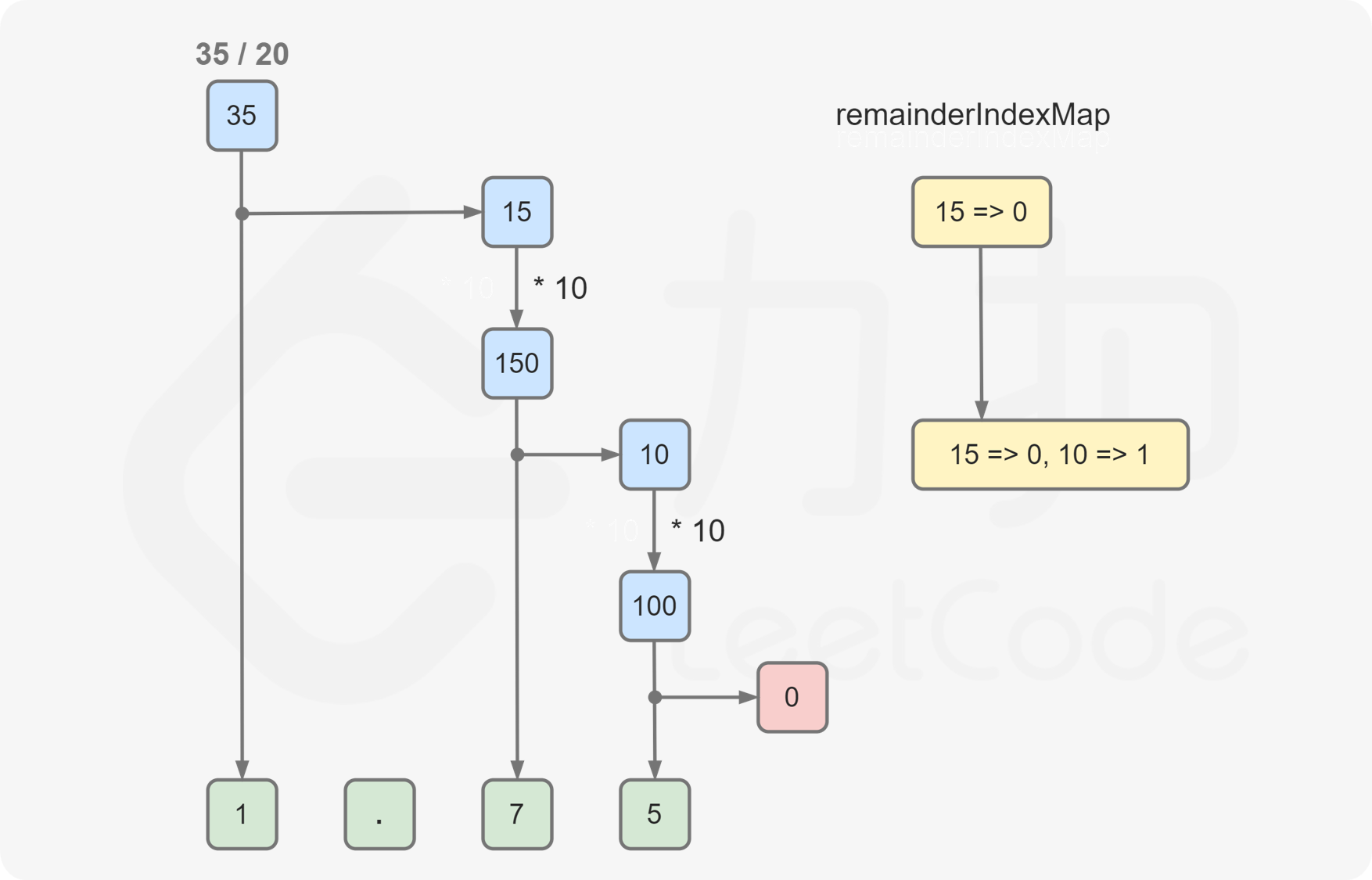
计算小数部分时，每次将余数乘以 \(10\)，然后计算小数的下一位数字，并得到新的余数。

重复上述操作直到余数变成 \(0\) 或者找到循环节。

如果余数变成 \(0\)，则结果是有限小数，将小数部分拼接到结果中。
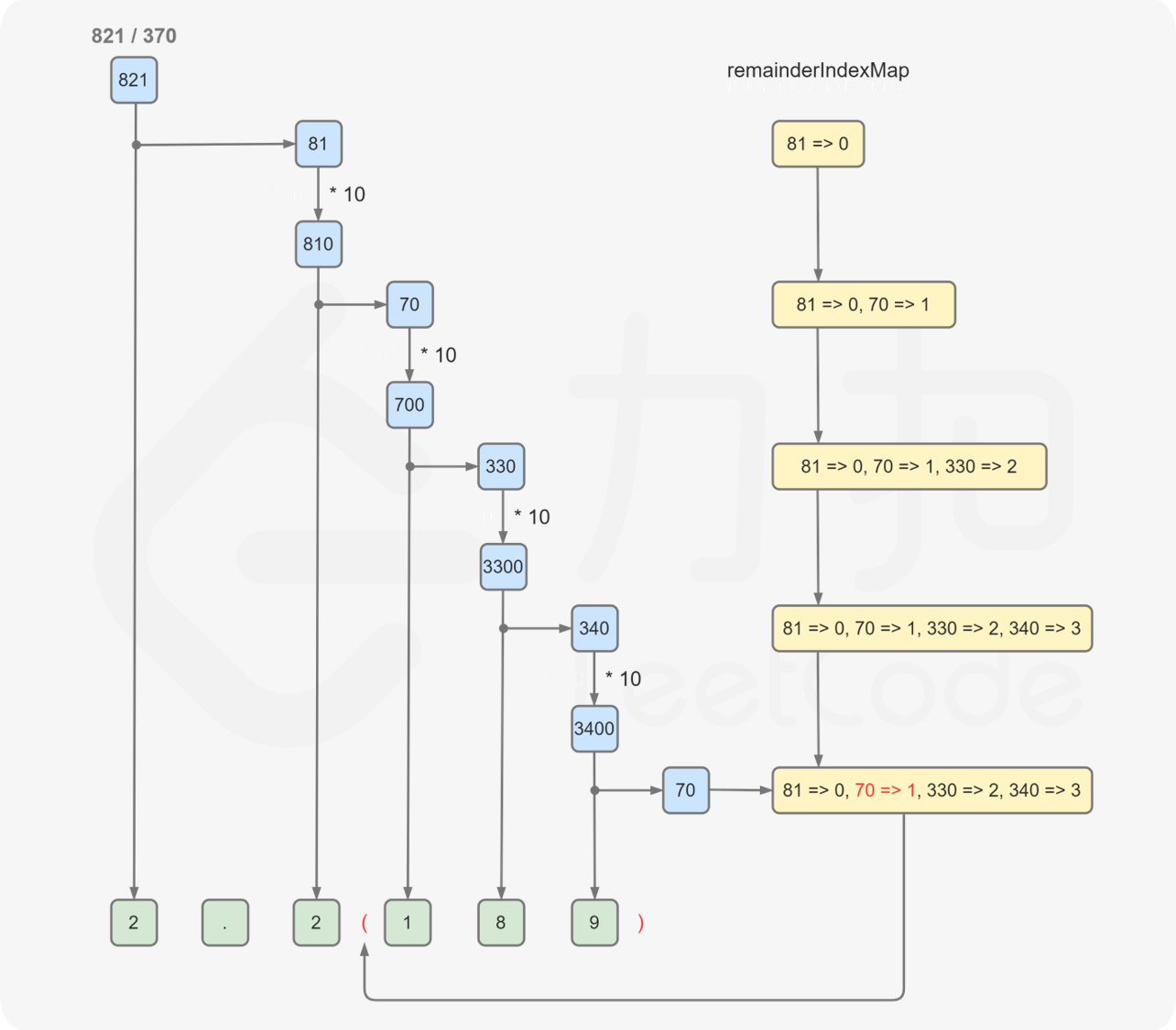
如果找到循环节，则找到循环节的开始位置和结束位置并加上括号，然后将小数部分拼接到结果中。

如何判断是否找到循环节？注意到对于相同的余数，计算得到的小数的下一位数字一定是相同的，因此如果计算过程中发现某一位的余数在之前已经出现过，则为找到循环节。为了记录每个余数是否已经出现过，需要使用哈希表存储每个余数在小数部分第一次出现的下标。

假设在计算小数部分的第 \(i\) 位之前，余数为 \( remainder_i \)，则在计算小数部分的第 \(i\) 位之后，余数为 \(\textit{remainder}_{i+1}\)。

假设存在下标 \(j\) 和 \(k\)，满足 \(j \le k\) 且 \(remainder_j = remainder_{k+1}\)，则小数部分的第 \(k+1\) 位和小数部分的第 \(j\) 位相同，因此小数部分的第 \(j\) 位到第 \(k\) 位是一个循环节。在计算小数部分的第 \(k\) 位之后就会发现这个循环节的存在，因此在小数部分的第 \(j\) 位之前加上左括号，在小数部分的末尾（即第 \(k\) 位之后）加上右括号。

fig1

fig2

class Solution {
public:
    string fractionToDecimal(int numerator, int denominator) {
        long numeratorLong = numerator;
        long denominatorLong = denominator;
        if (numeratorLong % denominatorLong == 0) {
            return to_string(numeratorLong / denominatorLong);
        }

        string ans;
        if (numeratorLong < 0 ^ denominatorLong < 0) {
            ans.push_back('-');
        }

        // 整数部分
        numeratorLong = abs(numeratorLong);
        denominatorLong = abs(denominatorLong);
        long integerPart = numeratorLong / denominatorLong;
        ans += to_string(integerPart);
        ans.push_back('.');

        // 小数部分
        string fractionPart;
        unordered_map<long, int> remainderIndexMap;
        long remainder = numeratorLong % denominatorLong;
        int index = 0;
        while (remainder != 0 && !remainderIndexMap.count(remainder)) {
            remainderIndexMap[remainder] = index;
            remainder *= 10;
            fractionPart += to_string(remainder / denominatorLong);
            remainder %= denominatorLong;
            index++;
        }
        if (remainder != 0) { // 有循环节
            int insertIndex = remainderIndexMap[remainder];
            fractionPart = fractionPart.substr(0,insertIndex) + '(' + fractionPart.substr(insertIndex);
            fractionPart.push_back(')');
        }
        ans += fractionPart;

        return ans;
    }
};

复杂度分析

时间复杂度：\(O(l)\)，其中 \(l\) 是答案字符串的长度，这道题中 \(l \le 10^4\)。对于答案字符串中的每一个字符，计算时间都是 \(O(1)\)。
空间复杂度：\(O(l)\)，其中 \(l\) 是答案字符串的长度，这道题中 \(l \le 10^4\)。空间复杂度主要取决于答案字符串和哈希表，哈希表中的每个键值对所对应的下标各不相同，因此键值对的数量不会超过 \(l\)

azarasi / LeetCode 166. Fraction to Recurring Decimal

题解