力扣数据中心有 n 台服务器,分别按从 0 到 n-1 的方式进行了编号。它们之间以「服务器到服务器」点对点的形式相互连接组成了一个内部集群,其中连接 connections 是无向的。从形式上讲,connections[i] = [a, b] 表示服务器 a 和 b 之间形成连接。任何服务器都可以直接或者间接地通过网络到达任何其他服务器。
「关键连接」 是在该集群中的重要连接,也就是说,假如我们将它移除,便会导致某些服务器无法访问其他服务器。
请你以任意顺序返回该集群内的所有 「关键连接」。
示例 1:
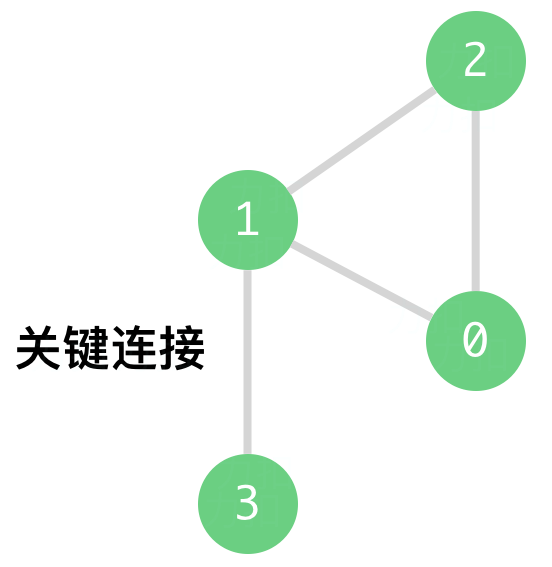
输入:n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
输出:[[1,3]]
解释:[[3,1]] 也是正确的。
示例 2:
输入:n = 2, connections = [[0,1]]
输出:[[0,1]]
提示:
- \(1 <= n <= 10^5\)
- \(n-1 <= connections.length <= 10^5\)
connections[i][0] != connections[i][1]- 不存在重复的连接
题解
开门见山,我们直接引出 Tarjan 算法在求解无向图的割点与桥的工作原理。
时间戳
时间戳是用来标记图中每个节点在进行深度优先搜索时被访问的时间顺序,当然,你可以理解成一个序号(这个序号由小到大),用 dfn[x] 来表示。
搜索树
在无向图中,我们以某一个节点 x 出发进行深度优先搜索,每一个节点只访问一次,所有被访问过的节点与边构成一棵树,我们可以称之为“无向连通图的搜索树”。
追溯值
追溯值用来表示从当前节点 x 作为搜索树的根节点出发,能够访问到的所有节点中,时间戳最小的值 —— low[x]。那么,我们要限定下什么是“能够访问到的所有节点”?,其需要满足下面的条件之一即可:
- 以 x 为根的搜索树的所有节点
- 通过一条非搜索树上的边,能够到达搜索树的所有节点
在一张无向图中,判断边 e (其对应的两个节点分别为 u 与 v)是否为桥,需要其满足如下条件即可:dfn[u] < low[v]
它代表的是节点 u 被访问的时间,要优先于(小于)以下这些节点被访问的时间 —— low[v] 。
- 以节点 v 为根的搜索树中的所有节点
- 通过一条非搜索树上的边,能够到达搜索树的所有节点(在追溯值内容中有所解释)
是不是上面的两个条件很眼熟?对,其实就是前文提到的追溯值 —— low[v]。
class Solution {
public:
void tarjan(int prev, int &step, vector<int> &dfn, int node, vector<unordered_set<int>> &g, vector<int> &low, vector<vector<int>> &ans) {
dfn[node] = step;
low[node] = step;
for(auto &next: g[node]) {
if(dfn[next] == -1) {
tarjan(node, ++step, dfn, next, g, low, ans);
}
if(next != prev) {
low[node] = min(low[node], low[next]);
}
if(dfn[node] < low[next]) {
ans.push_back({node, next});
}
}
}
vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
vector<unordered_set<int>> g(n);
for(auto &conn: connections) {
g[conn[0]].insert(conn[1]);
g[conn[1]].insert(conn[0]);
}
vector<vector<int>> ans;
vector<int> dfn(n, -1);
vector<int> low(n, -1);
unordered_set<int> vis;
int step = 0;
for(int i = 0; i < n; i++) {
if(dfn[i] == -1) {
step = 0;
tarjan(-1, step, dfn, i, g, low, ans);
}
}
return ans;
}
};