给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1]
输出:[0]
示例 3:
输入:nums = [-1,-1]
输出:[0,0]
提示:
- \(1 <= nums.length <= 10^5\)
- \(-10^4 <= nums[i] <= 10^4\)
题解
方法一:离散化树状数组
预备知识
「树状数组」是一种可以动态维护序列前缀和的数据结构,它的功能是:
- 单点更新
update(i, v): 把序列 \(i\) 位置的数加上一个值 \(v\),在该题中 \(v = 1\) - 区间查询
query(i): 查询序列 \([1 \cdots i]\) 区间的区间和,即 \(i\) 位置的前缀和
修改和查询的时间代价都是 \(O(\log n)\),其中 \(n\) 为需要维护前缀和的序列的长度。
思路与算法
记题目给定的序列为 \(a\),我们规定 \(a_i\) 的取值集合为 \(a\) 的「值域」。我们用桶来表示值域中的每一个数,桶中记录这些数字出现的次数。假设\(a = {5, 5, 2, 3, 6}\)那么遍历这个序列得到的桶是这样的:
index -> 1 2 3 4 5 6 7 8 9
value -> 0 1 1 0 2 1 0 0 0
转化为动态维护前缀和问题
记 value 序列为 \(v\),我们可以看出它第 \(i - 1\) 位的前缀和表示「有多少个数比 \(i\) 小」。那么我们可以从后往前遍历序列 \(a\),记当前遍历到的元素为 \(a_i\),我们把 \(a_i\) 对应的桶的值自增 \(1\),记 \(a_i = p\),把 \(v\) 序列 \(p - 1\) 位置的前缀和加入到答案中算贡献。为什么这么做是对的呢,因为我们在循环的过程中,我们把原序列分成了两部分,后半部部分已经遍历过(已入桶),前半部分是待遍历的(未入桶),那么我们求到的 \(p - 1\) 位置的前缀和就是「已入桶」的元素中比 \(p\) 小的元素的个数总和。这种动态维护前缀和的问题我们可以用「树状数组」来解决。
用离散化优化空间
我们显然可以用数组来实现这个桶,可问题是如果 \(a_i\) 中有很大的元素,比如 \(10^9\),我们就要开一个大小为 \(10^9\) 的桶,内存中是存不下的。这个桶数组中很多位置是 \(0\),有效位置是稀疏的,我们要想一个办法让有效的位置全聚集到一起,减少无效位置的出现,这个时候我们就需要用到一个方法——离散化。离散化的方法有很多,但是目的是一样的,即把原序列的值域映射到一个连续的整数区间,并保证它们的偏序关系不变。 这里我们将原数组去重后排序,原数组每个数映射到去重排序后这个数对应位置的下标,我们称这个下标为这个对应数字的 \(\rm id\)。已知数字获取 \(\rm id\) 可以在去重排序后的数组里面做二分查找,已知 \(\rm id\) 获取数字可以直接把 \(\rm id\) 作为下标访问去重排序数组的对应位置。大家可以参考代码和图来理解这个过程。
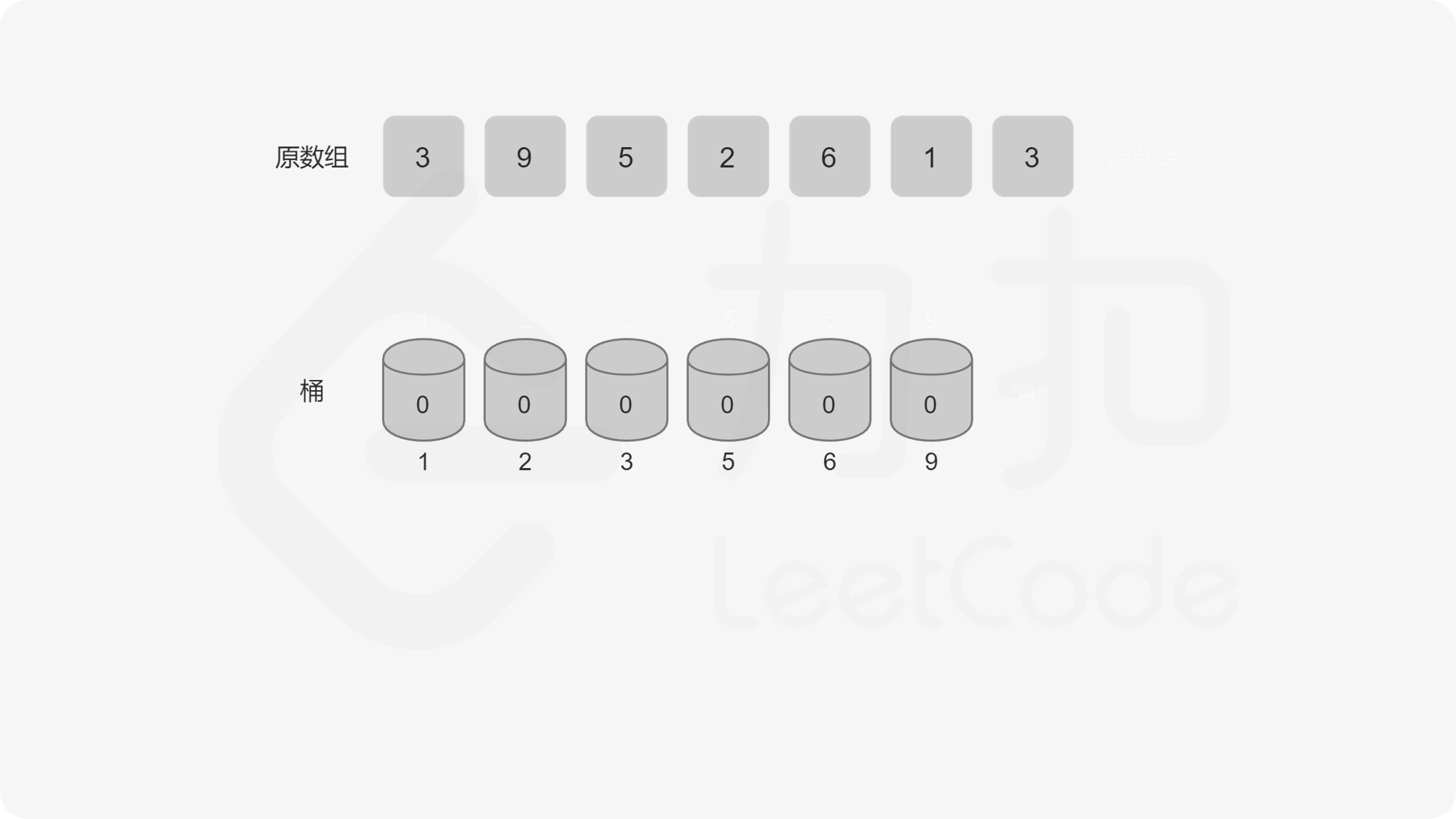
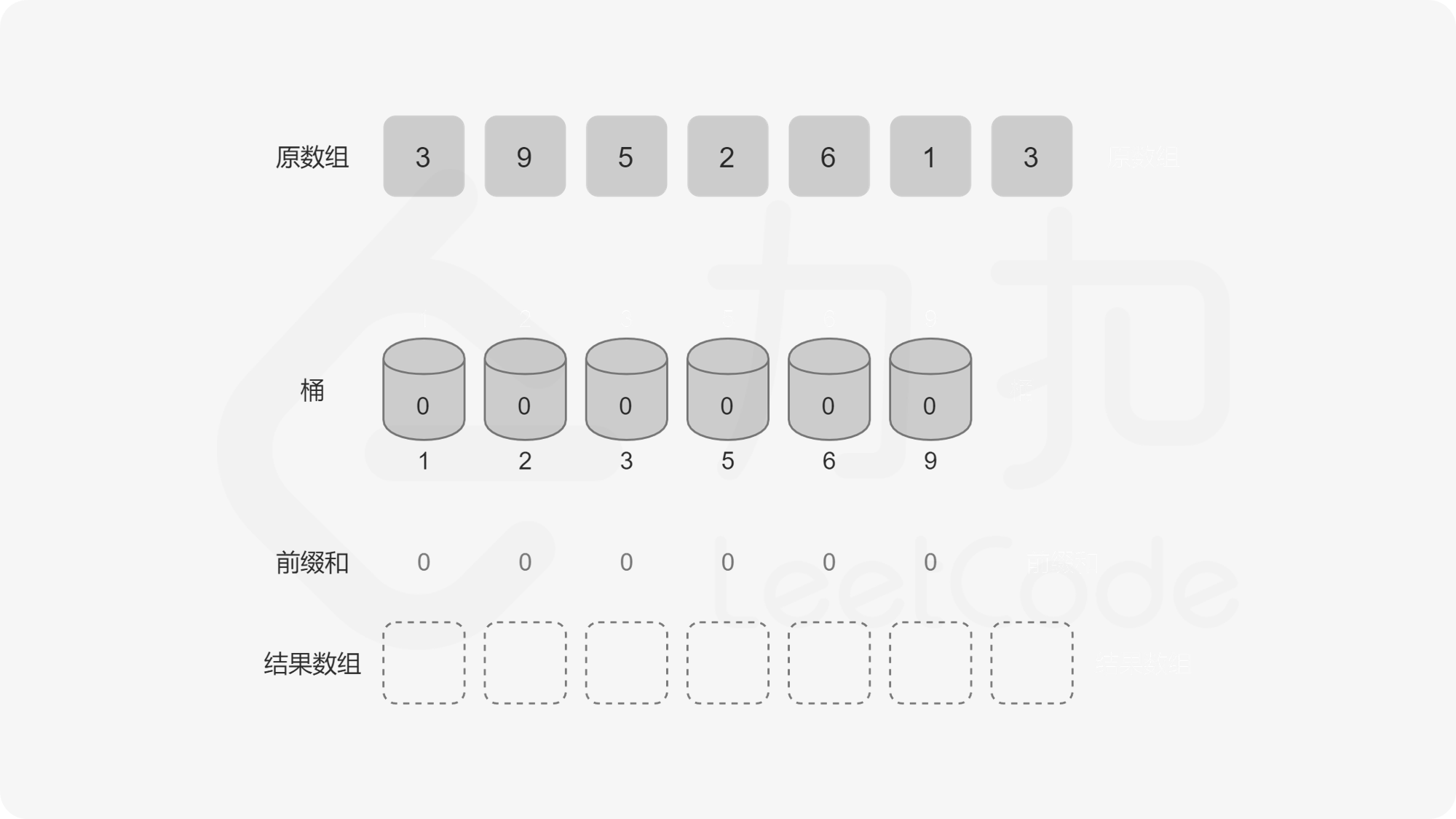
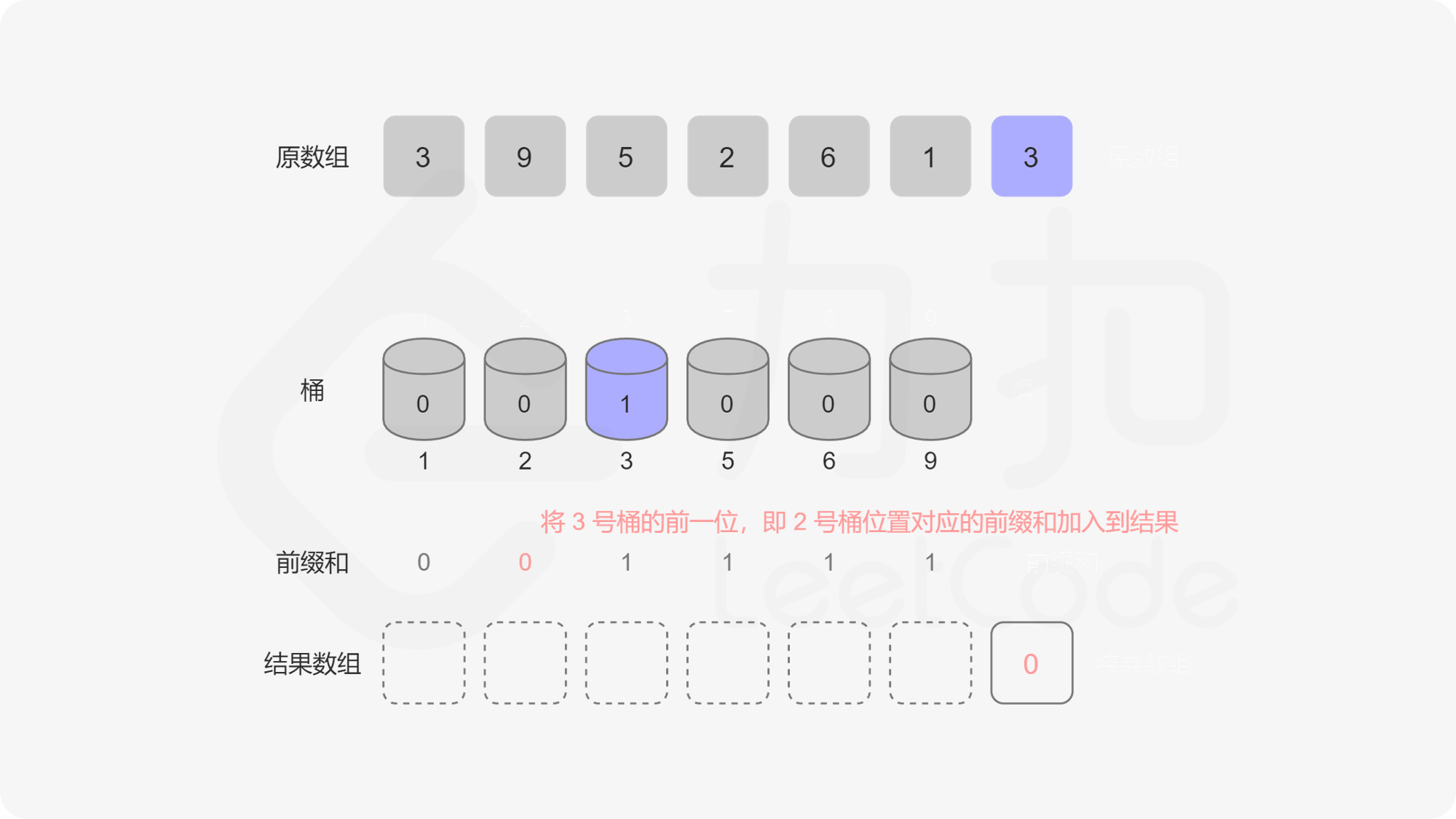
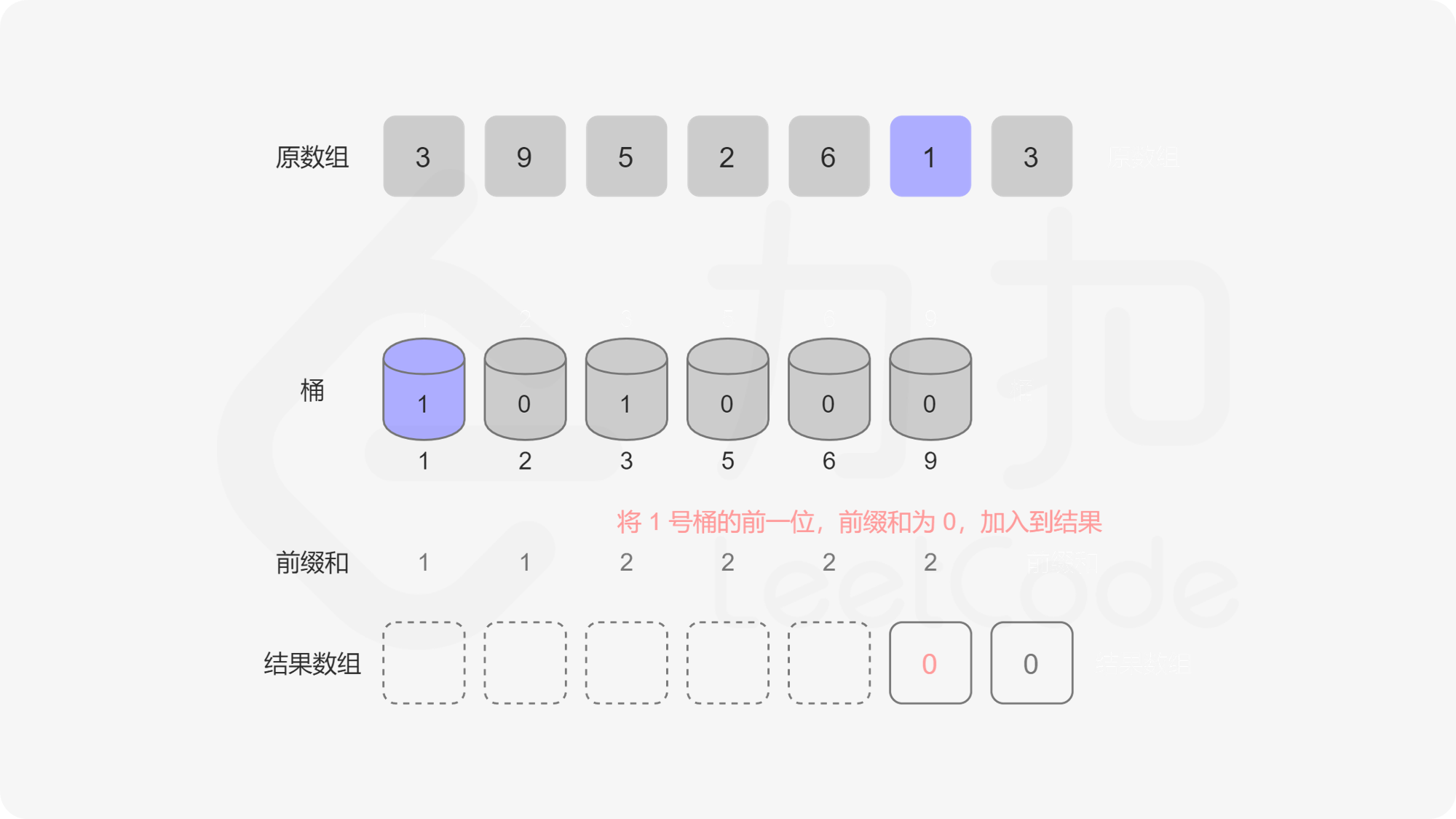
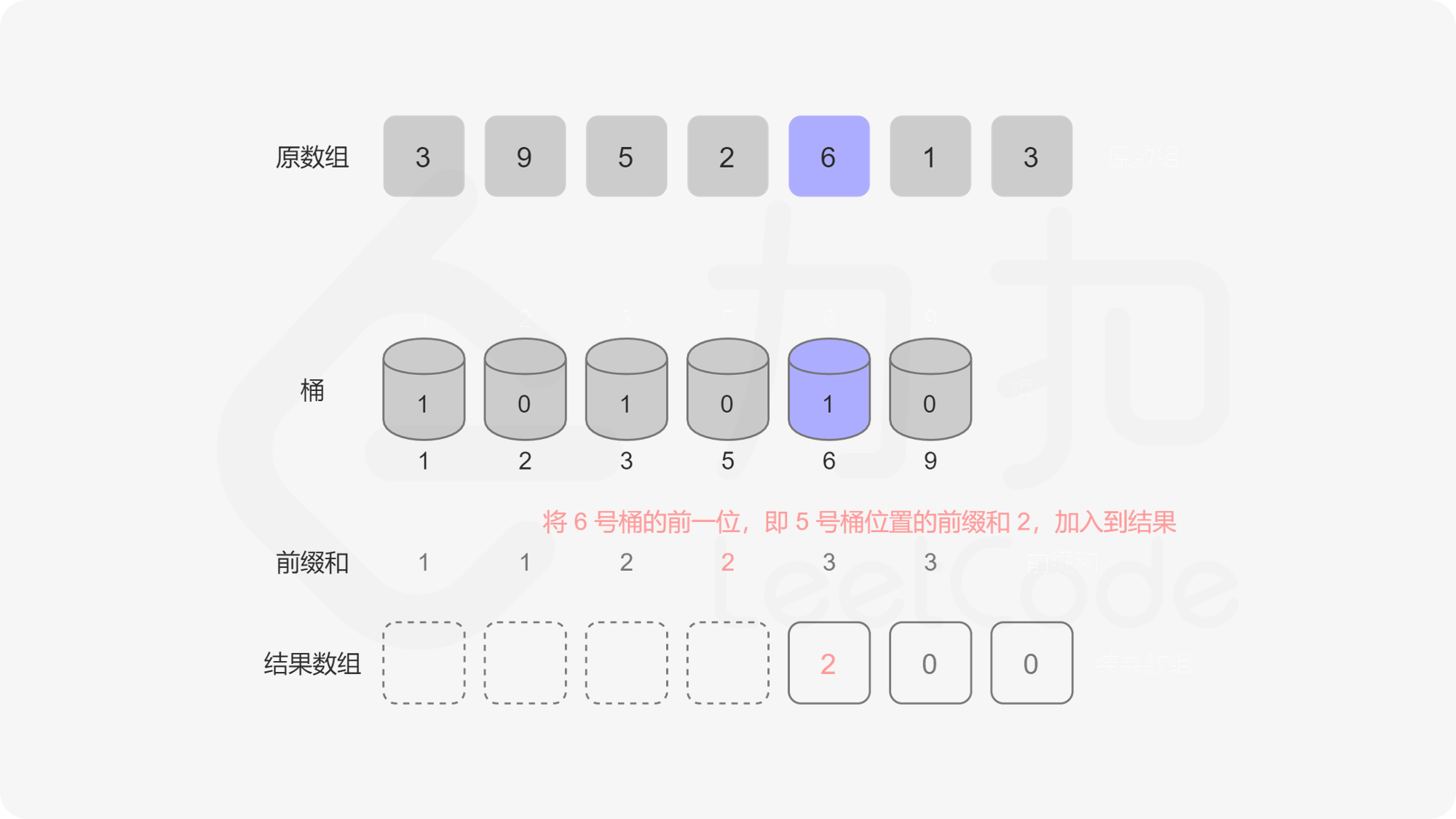
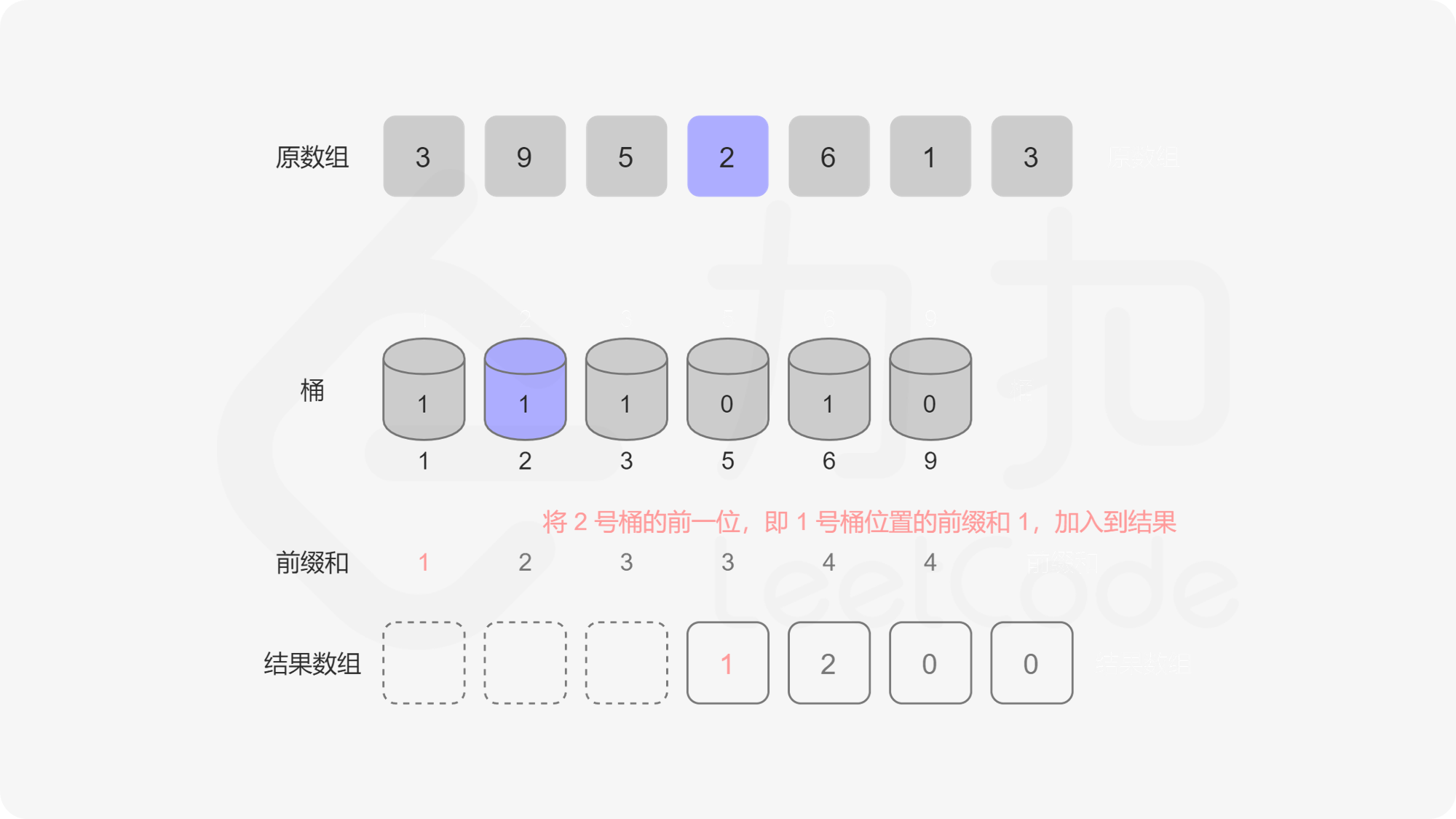
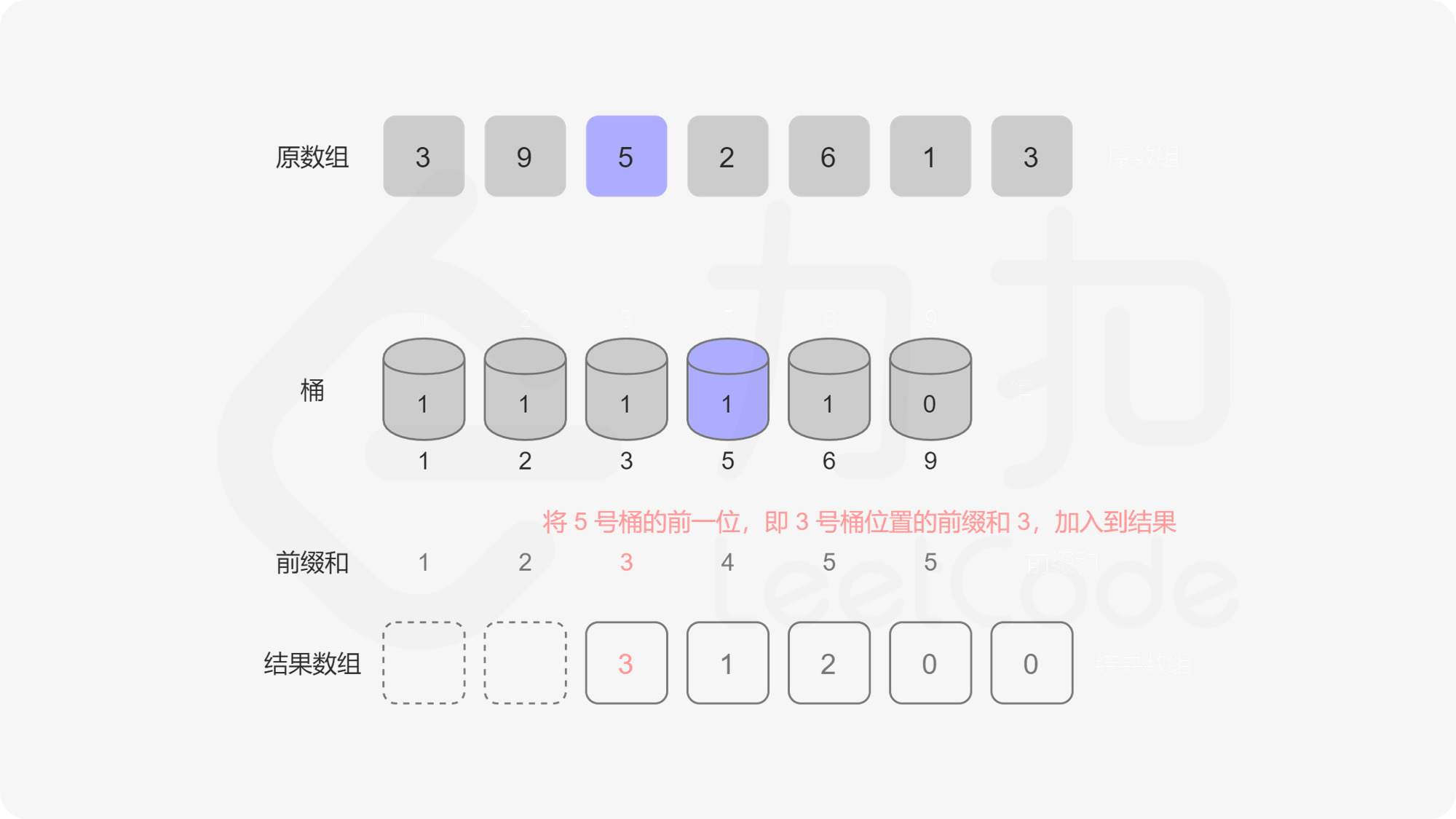
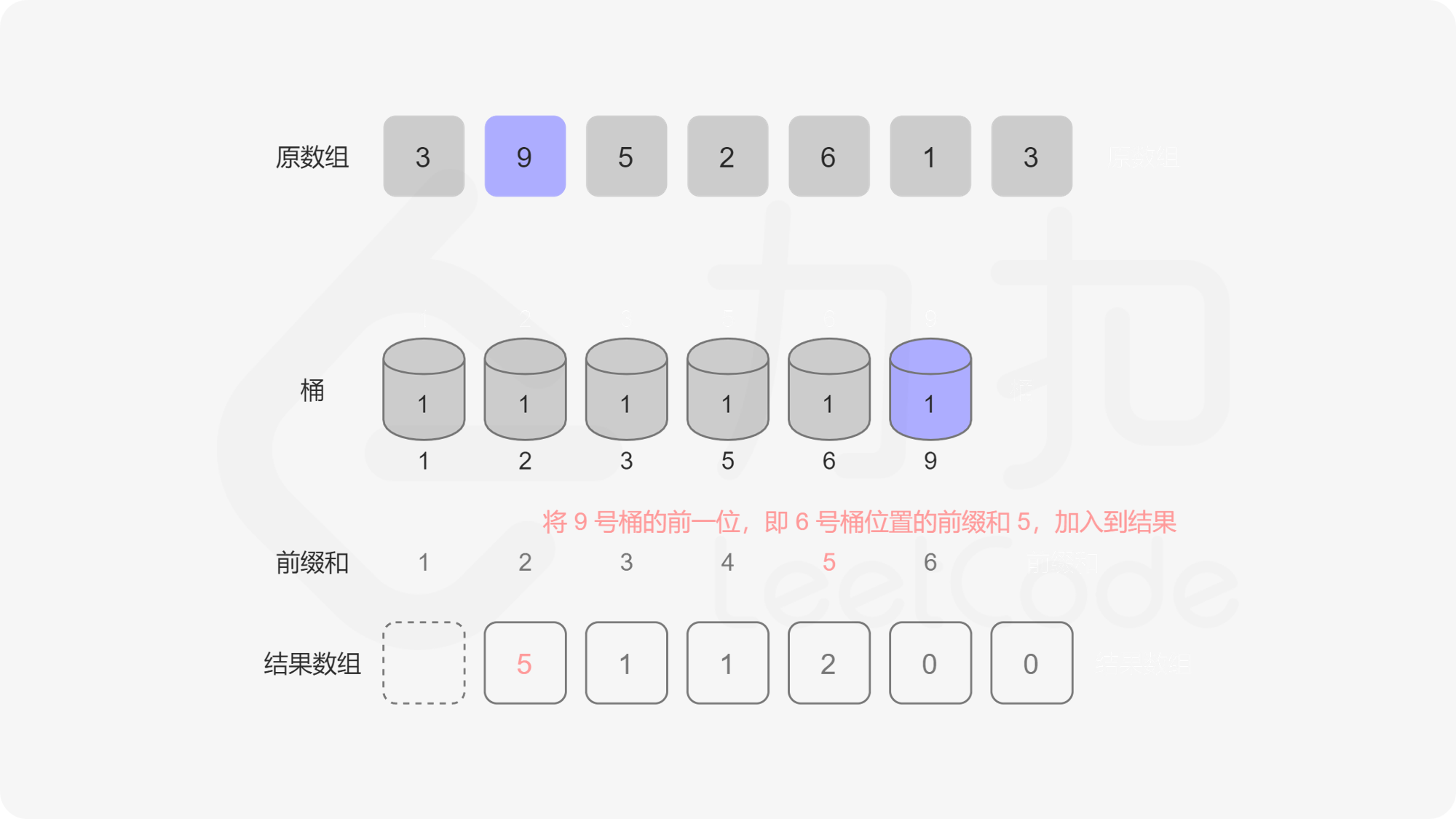
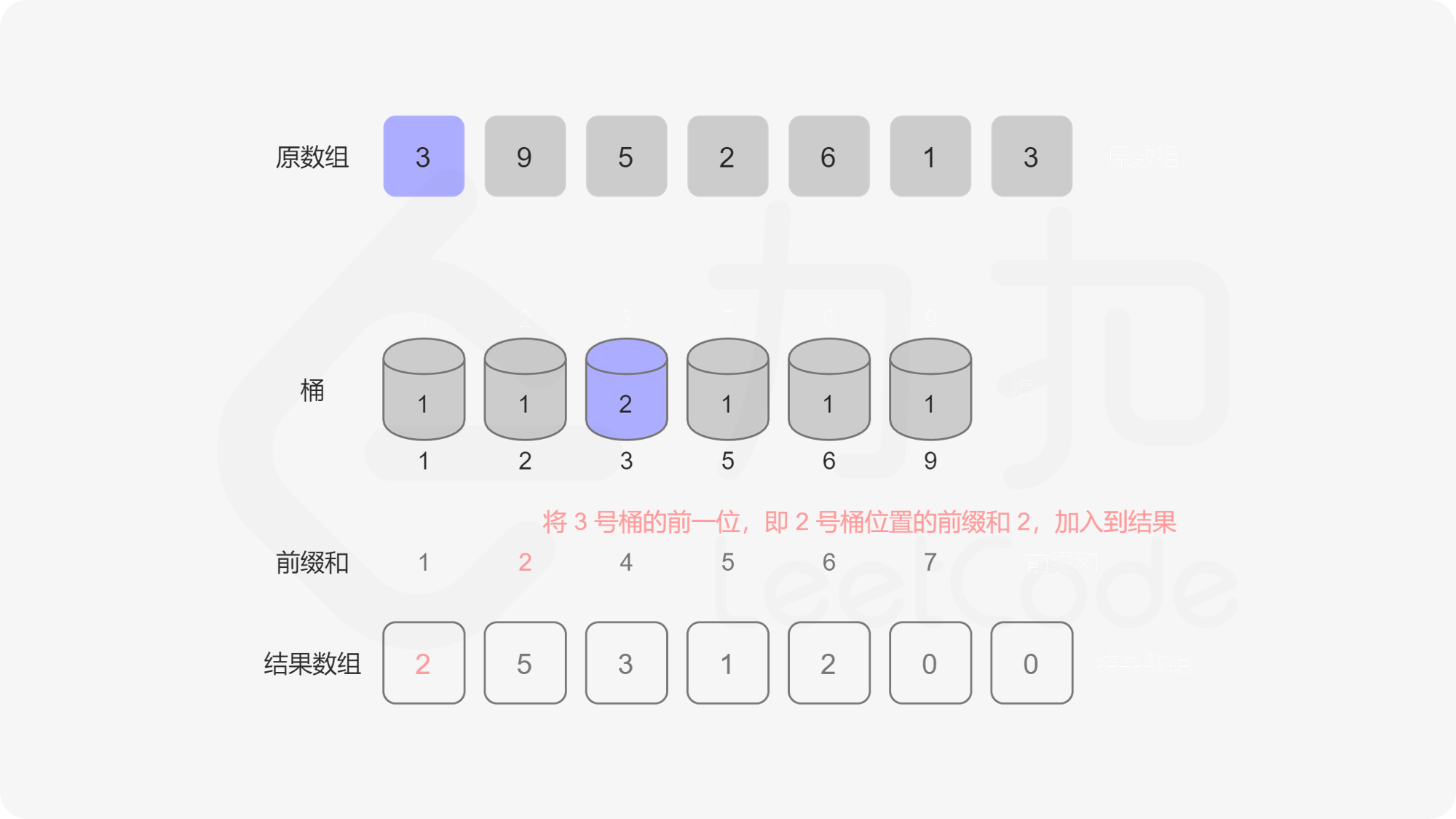

其实,计算每个数字右侧小于当前元素的个数,这个问题我们在「剑指 Offer 51. 数组中的逆序对」题解的「方法二:离散化树状数组」中遇到过,在统计逆序对的时候,只需要统计每个位置右侧小于当前元素的个数,再对它们求和,就可以得到逆序对的总数。这道逆序对的题可以作为本题的补充练习。
代码如下。
代码
class Solution {
private:
vector<int> c;
vector<int> a;
void Init(int length) {
c.resize(length, 0);
}
int LowBit(int x) {
return x & (-x);
}
void Update(int pos) {
while (pos < c.size()) {
c[pos] += 1;
pos += LowBit(pos);
}
}
int Query(int pos) {
int ret = 0;
while (pos > 0) {
ret += c[pos];
pos -= LowBit(pos);
}
return ret;
}
void Discretization(vector<int>& nums) {
a.assign(nums.begin(), nums.end());
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
}
int getId(int x) {
return lower_bound(a.begin(), a.end(), x) - a.begin() + 1;
}
public:
vector<int> countSmaller(vector<int>& nums) {
vector<int> resultList;
Discretization(nums);
Init(nums.size() + 5);
for (int i = (int)nums.size() - 1; i >= 0; --i) {
int id = getId(nums[i]);
resultList.push_back(Query(id - 1));
Update(id);
}
reverse(resultList.begin(), resultList.end());
return resultList;
}
};
复杂度分析
假设题目给出的序列长度为 \(n\)。
- 时间复杂度:我们梳理一下这个算法的流程,这里离散化使用哈希表去重,然后再对去重的数组进行排序,时间代价为 \(O(n \log n)\);初始化树状数组的时间代价是 \(O(n)\);通过值获取离散化 \(\rm id\) 的操作单次时间代价为 \(O(\log n)\);对于每个序列中的每个元素,都会做一次查询 \(\rm id\)、单点修改和前缀和查询,总的时间代价为 \(O(n \log n)\)。故渐进时间复杂度为 \(O(n \log n)\)。
- 空间复杂度:这里用到的离散化数组、树状数组、哈希表的空间代价都是 \(O(n)\),故渐进空间复杂度为 \(O(n)\)。
方法二:归并排序
预备知识
这里假设读者已经知道如何使用归并排序的方法计算序列的逆序对数,如果读者还不知道的话可以参考 「剑指 Offer 51. 数组中的逆序对」 的官方题解哦。
思路与算法
我们发现「离散化树状数组」的方法几乎于 「剑指 Offer 51. 数组中的逆序对」 中的完全相同,那么我们可不可以借鉴逆序对问题中的归并排序的方法呢?
我们还是要在「归并排序」的「并」中做文章。我们通过一个实例来看看。假设我们有两个已排序的序列等待合并,分别是 \(L = { 8, 12, 16, 22, 100 }\) 和 \(R = { 7, 26, 55, 64, 91 }\)。一开始我们用指针 lPtr = 0 指向 \(L\) 的头部,rPtr = 0 指向 \(R\) 的头部。记已经合并好的部分为 \(M\)。
L = [8, 12, 16, 22, 100] R = [7, 26, 55, 64, 91] M = []
| |
lPtr rPtr
我们发现 lPtr 指向的元素大于 rPtr 指向的元素,于是把 rPtr 指向的元素放入答案,并把 rPtr 后移一位。
L = [8, 12, 16, 22, 100] R = [7, 26, 55, 64, 91] M = [7]
| |
lPtr rPtr
接着我们继续合并:
L = [8, 12, 16, 22, 100] R = [7, 26, 55, 64, 91] M = [8, 9]
| |
lPtr rPtr
此时 lPtr 比 rPtr 小,把 lPtr 对应的数加入答案。如果我们要统计 \(8\) 的右边比 \(8\) 小的元素,这里 \(7\) 对它做了一次贡献。如果带合并的序列 \(L = { 8, 12, 16, 22, 100 }\),\(R = { 7, 7, 7, 26, 55, 64, 91}\),那么一定有一个时刻,lPtr 和 rPtr 分别指向这些对应的位置:
L = [8, 12, 16, 22, 100] R = [7, 7, 7, 26, 55, 64, 91] M = [7, 7, 7]
| |
lPtr rPtr
下一步我们就是把 \(8\) 加入 \(M\) 中,此时三个 \(7\) 对 \(8\) 的右边比 \(8\) 小的元素的贡献为 \(3\)。以此类推,我们可以一边合并一边计算 \(R\) 的头部到 rPtr 前一个数字对当前 lPtr 指向的数字的贡献。
我们发现用这种「算贡献」的思想在合并的过程中计算逆序对的数量的时候,只在 lPtr 右移的时候计算,是基于这样的事实:当前 lPtr 指向的数字比 rPtr 小,但是比 \(R\) 中 [0 ... rPtr - 1] 的其他数字大,[0 ... rPtr - 1] 的数字是在 lPtr 右边但是比 lPtr 对应数小的数字,贡献为这些数字的个数。
但是我们又遇到了新的问题,在「并」的过程中 \(8\) 的位置一直在发生改变,我们应该把计算的贡献保存到哪里呢?这个时候我们引入一个新的数组,来记录每个数字对应的原数组中的下标,例如:
a = [8, 9, 1, 5, 2]
index = [0, 1, 2, 3, 4]
排序的时候原数组和这个下标数组同时变化,则排序后我们得到这样的两个数组:
a = [1, 2, 5, 8, 9]
index = [2, 4, 3, 0, 1]
我们用一个数组 ans 来记录贡献。我们对某个元素计算贡献的时候,如果它对应的下标为 p,我们只需要在 ans[p] 上加上贡献即可。
大家可以参考代码来理解这个过程。
代码
class Solution {
private int[] index;
private int[] temp;
private int[] tempIndex;
private int[] ans;
public List<Integer> countSmaller(int[] nums) {
this.index = new int[nums.length];
this.temp = new int[nums.length];
this.tempIndex = new int[nums.length];
this.ans = new int[nums.length];
for (int i = 0; i < nums.length; ++i) {
index[i] = i;
}
int l = 0, r = nums.length - 1;
mergeSort(nums, l, r);
List<Integer> list = new ArrayList<Integer>();
for (int num : ans) {
list.add(num);
}
return list;
}
public void mergeSort(int[] a, int l, int r) {
if (l >= r) {
return;
}
int mid = (l + r) >> 1;
mergeSort(a, l, mid);
mergeSort(a, mid + 1, r);
merge(a, l, mid, r);
}
public void merge(int[] a, int l, int mid, int r) {
int i = l, j = mid + 1, p = l;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) {
temp[p] = a[i];
tempIndex[p] = index[i];
ans[index[i]] += (j - mid - 1);
++i;
++p;
} else {
temp[p] = a[j];
tempIndex[p] = index[j];
++j;
++p;
}
}
while (i <= mid) {
temp[p] = a[i];
tempIndex[p] = index[i];
ans[index[i]] += (j - mid - 1);
++i;
++p;
}
while (j <= r) {
temp[p] = a[j];
tempIndex[p] = index[j];
++j;
++p;
}
for (int k = l; k <= r; ++k) {
index[k] = tempIndex[k];
a[k] = temp[k];
}
}
}
复杂度分析
- 时间复杂度:\(O(n \log n)\),即归并排序的时间复杂度。
- 空间复杂度:\(O(n)\),这里归并排序的临时数组、下标映射数组以及答案数组的空间代价均为 \(O(n)\)。