给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
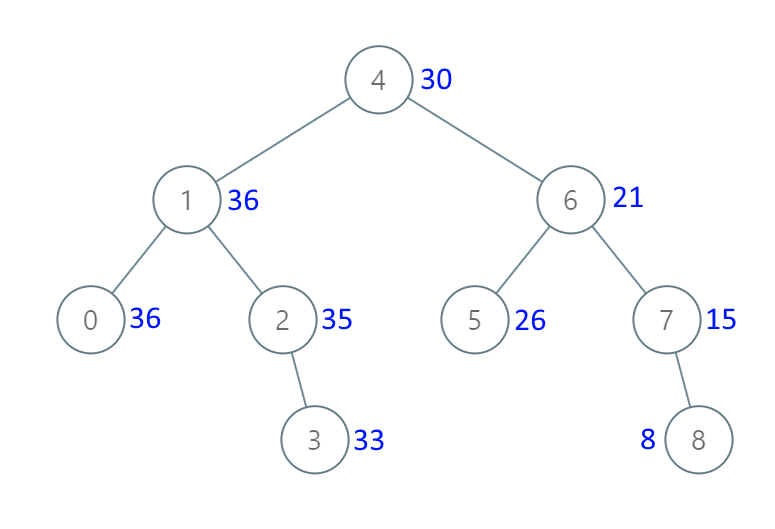
输入: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入: root = [0,null,1]
输出: [1,null,1]
示例 3:
输入: root = [1,0,2]
输出: [3,3,2]
示例 4:
输入: root = [3,2,4,1]
输出: [7,9,4,10]
提示:
- \(树中的节点数介于 0 和 10^4 之间。\)
- \(每个节点的值介于 -10^4 和 10^4 之间。\)
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
- 哪种遍历方法能将所有节点按排序组织起来?
struct FriendTreeNode {
int sum;
int val;
FriendTreeNode * left;
FriendTreeNode * right;
TreeNode * friend_node;
explicit FriendTreeNode(int x, TreeNode * friend_node): sum(x), val(0), left(nullptr), right(nullptr),
friend_node(friend_node) {}
};
class Solution {
public:
static TreeNode * convertBST(TreeNode * root);
static FriendTreeNode * copy(TreeNode * );
static void get_sum(FriendTreeNode * );
static void convert(FriendTreeNode * );
};
TreeNode * Solution::convertBST(TreeNode * root) {
if (root == nullptr) {
return nullptr;
}
FriendTreeNode * sum = Solution::copy(root);
get_sum(sum);
sum -> val = sum -> sum - (sum -> left == nullptr ? 0 : sum -> left -> sum);
Solution::convert(sum);
return root;
}
FriendTreeNode * Solution::copy(TreeNode * node) {
auto * ret = new FriendTreeNode(node -> val, node);
if (node -> left != nullptr) {
ret -> left = Solution::copy(node -> left);
}
if (node -> right != nullptr) {
ret -> right = Solution::copy(node -> right);
}
return ret;
}
void Solution::get_sum(FriendTreeNode * node) {
if (node -> left != nullptr) {
get_sum(node -> left);
node -> sum += node -> left -> sum;
}
if (node -> right != nullptr) {
get_sum(node -> right);
node -> sum += node -> right -> sum;
}
}
void Solution::convert(FriendTreeNode * sum_node) {
if (sum_node -> right != nullptr) {
sum_node -> right -> val = sum_node -> val - sum_node -> friend_node -> val -
(sum_node -> right -> left == nullptr ? 0 : sum_node -> right -> left -> sum);
Solution::convert(sum_node -> right);
}
if (sum_node -> left != nullptr) {
sum_node -> left -> val = sum_node -> val + sum_node -> left -> friend_node -> val +
(sum_node -> left -> right == nullptr ? 0 : sum_node -> left -> right -> sum);
Solution::convert(sum_node -> left);
}
sum_node -> friend_node -> val = sum_node -> val;
}